y-y-e-2x-sin-e-x- – Tinku Tara

Question Number 131086 by EDWIN88 last updated on 01/Feb/21

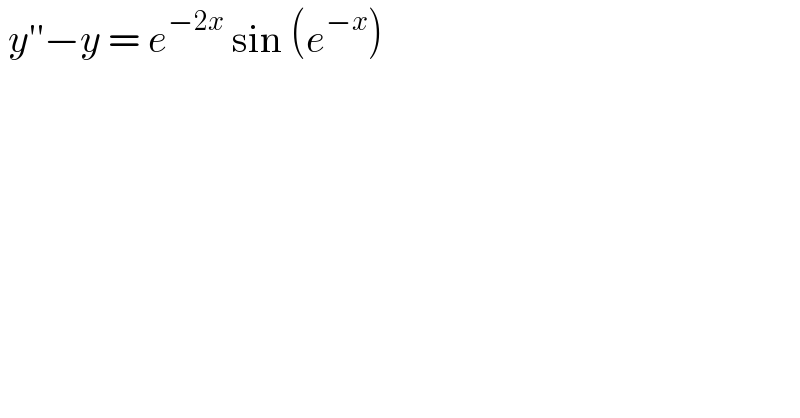
$$\:{y}''−{y}\:=\:{e}^{−\mathrm{2}{x}} \:\mathrm{sin}\:\left({e}^{−{x}} \right)\: \\ $$

Answered by liberty last updated on 01/Feb/21

[ D^2 −1 ]y = e^(−2x) sin (e^(−x) ) (D−1)(D+1)y=e^(−2x) sin (e^(−x) ) (D−1)[e^x (D+1)y ] = e^(−x) sin (e^(−x) ) (D−1)D(e^x y)=e^(−x) sin (e^(−x) ) (D−1)e^x y = ∫e^(−x) sin (e^(−x) )dx (D−1)e^x y = cos (e^(−x) )+C_1 (D−1)y = e^(−x) cos (e^(−x) )+C_1 e^(−x) (D−1)e^(−x) y = e^(−2x) +C_1 e^(−2x) D(e^(−x) y) = e^(−2x) +C_1 e^(−2x) e^(−x) y = ∫(e^(−2x) +C_1 e^(−2x) )dx y = e^x [ −e^(−x) sin (e^(−x) )−cos (e^(−x) )−(1/2)C_1 e^(−2x) +C_2 ]

$$\left[\:\mathrm{D}^{\mathrm{2}} −\mathrm{1}\:\right]\mathrm{y}\:=\:\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\left(\mathrm{D}+\mathrm{1}\right)\mathrm{y}=\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\left[\mathrm{e}^{\mathrm{x}} \left(\mathrm{D}+\mathrm{1}\right)\mathrm{y}\:\right]\:=\:\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\mathrm{D}\left(\mathrm{e}^{\mathrm{x}} \mathrm{y}\right)=\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \mathrm{y}\:=\:\int\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx} \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \mathrm{y}\:=\:\mathrm{cos}\:\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\mathrm{y}\:=\:\mathrm{e}^{−\mathrm{x}} \mathrm{cos}\:\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \\ $$$$\left(\mathrm{D}−\mathrm{1}\right)\mathrm{e}^{−\mathrm{x}} \mathrm{y}\:=\:\mathrm{e}^{−\mathrm{2x}} +\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{D}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{y}\right)\:=\:\mathrm{e}^{−\mathrm{2x}} +\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{e}^{−\mathrm{x}} \mathrm{y}\:=\:\int\left(\mathrm{e}^{−\mathrm{2x}} +\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} \right)\mathrm{dx} \\ $$$$\:\mathrm{y}\:=\:\mathrm{e}^{\mathrm{x}} \:\left[\:−\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{cos}\:\left(\mathrm{e}^{−\mathrm{x}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2x}} +\mathrm{C}_{\mathrm{2}} \:\right] \\ $$

Commented by EDWIN88 last updated on 01/Feb/21

$${waw}… \\ $$

Commented by EDWIN88 last updated on 01/Feb/21

զարմանալի

Answered by Ar Brandon last updated on 01/Feb/21

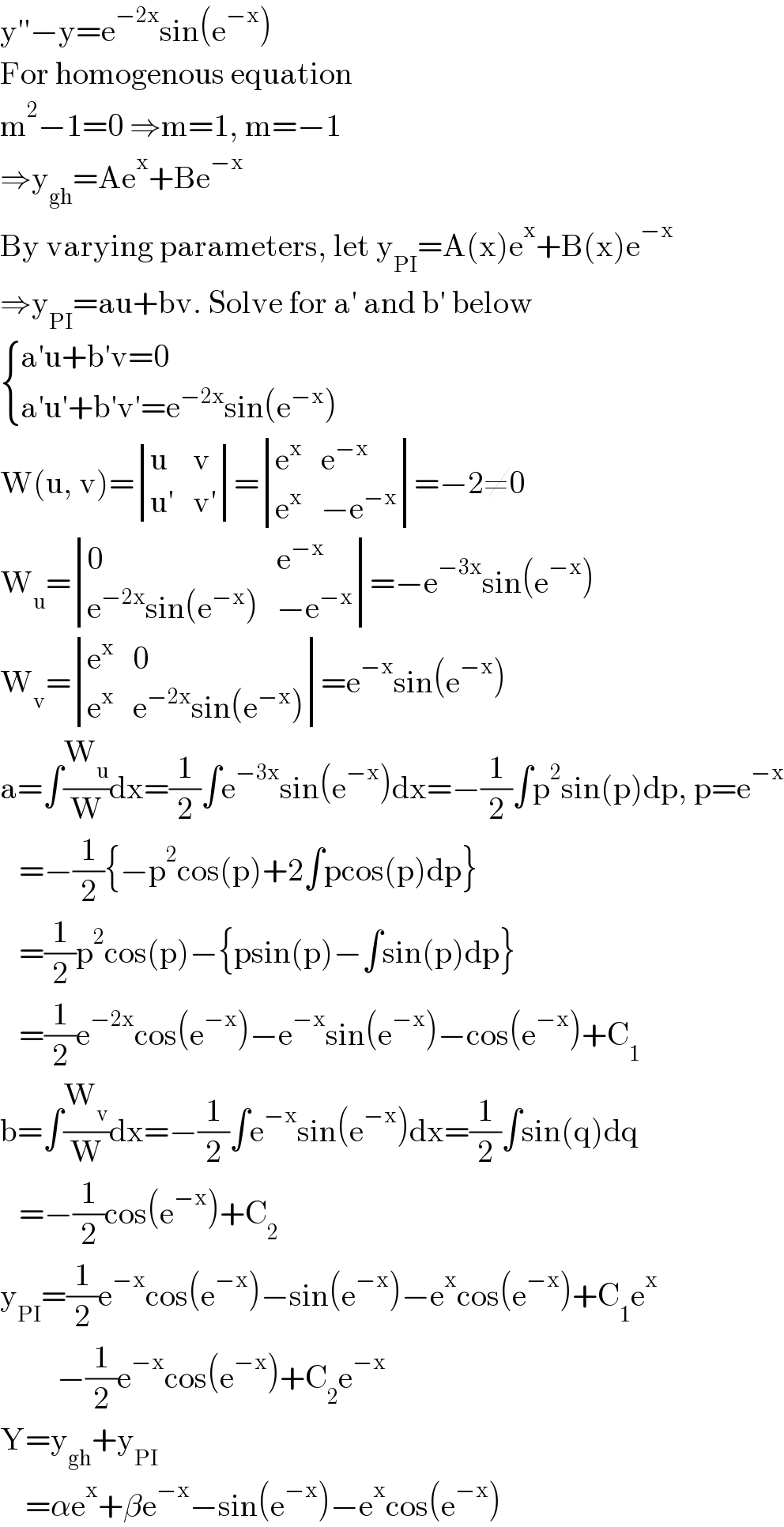
y′′−y=e^(−2x) sin(e^(−x) ) For homogenous equation m^2 −1=0 ⇒m=1, m=−1 ⇒y_(gh) =Ae^x +Be^(−x) By varying parameters, let y_(PI) =A(x)e^x +B(x)e^(−x) ⇒y_(PI) =au+bv. Solve for a′ and b′ below { ((a′u+b′v=0)),((a′u′+b′v′=e^(−2x) sin(e^(−x) ))) :} W(u, v)= determinant ((u,v),((u′),(v′)))= determinant ((e^x ,e^(−x) ),(e^x ,(−e^(−x) )))=−2≠0 W_u = determinant ((0,e^(−x) ),((e^(−2x) sin(e^(−x) )),(−e^(−x) )))=−e^(−3x) sin(e^(−x) ) W_v = determinant ((e^x ,0),(e^x ,(e^(−2x) sin(e^(−x) ))))=e^(−x) sin(e^(−x) ) a=∫(W_u /W)dx=(1/2)∫e^(−3x) sin(e^(−x) )dx=−(1/2)∫p^2 sin(p)dp, p=e^(−x) =−(1/2){−p^2 cos(p)+2∫pcos(p)dp} =(1/2)p^2 cos(p)−{psin(p)−∫sin(p)dp} =(1/2)e^(−2x) cos(e^(−x) )−e^(−x) sin(e^(−x) )−cos(e^(−x) )+C_1 b=∫(W_v /W)dx=−(1/2)∫e^(−x) sin(e^(−x) )dx=(1/2)∫sin(q)dq =−(1/2)cos(e^(−x) )+C_2 y_(PI) =(1/2)e^(−x) cos(e^(−x) )−sin(e^(−x) )−e^x cos(e^(−x) )+C_1 e^x −(1/2)e^(−x) cos(e^(−x) )+C_2 e^(−x) Y=y_(gh) +y_(PI) =αe^x +βe^(−x) −sin(e^(−x) )−e^x cos(e^(−x) )

$$\mathrm{y}''−\mathrm{y}=\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\mathrm{For}\:\mathrm{homogenous}\:\mathrm{equation} \\ $$$$\mathrm{m}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{m}=\mathrm{1},\:\mathrm{m}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{gh}} =\mathrm{Ae}^{\mathrm{x}} +\mathrm{Be}^{−\mathrm{x}} \\ $$$$\mathrm{By}\:\mathrm{varying}\:\mathrm{parameters},\:\mathrm{let}\:\mathrm{y}_{\mathrm{PI}} =\mathrm{A}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{B}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{x}} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{PI}} =\mathrm{au}+\mathrm{bv}.\:\mathrm{Solve}\:\mathrm{for}\:\mathrm{a}'\:\mathrm{and}\:\mathrm{b}'\:\mathrm{below} \\ $$$$\begin{cases}{\mathrm{a}'\mathrm{u}+\mathrm{b}'\mathrm{v}=\mathrm{0}}\\{\mathrm{a}'\mathrm{u}'+\mathrm{b}'\mathrm{v}'=\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)}\end{cases} \\ $$$$\mathrm{W}\left(\mathrm{u},\:\mathrm{v}\right)=\begin{vmatrix}{\mathrm{u}}&{\mathrm{v}}\\{\mathrm{u}'}&{\mathrm{v}'}\end{vmatrix}=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} }&{\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{e}^{\mathrm{x}} }&{−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=−\mathrm{2}\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{u}} =\begin{vmatrix}{\mathrm{0}}&{\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)}&{−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=−\mathrm{e}^{−\mathrm{3x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\mathrm{W}_{\mathrm{v}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} }&{\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} }&{\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)}\end{vmatrix}=\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$$$\mathrm{a}=\int\frac{\mathrm{W}_{\mathrm{u}} }{\mathrm{W}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{−\mathrm{3x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{p}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{p}\right)\mathrm{dp},\:\mathrm{p}=\mathrm{e}^{−\mathrm{x}} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{p}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{p}\right)+\mathrm{2}\int\mathrm{pcos}\left(\mathrm{p}\right)\mathrm{dp}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{p}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{p}\right)−\left\{\mathrm{psin}\left(\mathrm{p}\right)−\int\mathrm{sin}\left(\mathrm{p}\right)\mathrm{dp}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{b}=\int\frac{\mathrm{W}_{\mathrm{v}} }{\mathrm{W}}\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\left(\mathrm{q}\right)\mathrm{dq} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{PI}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}} \mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{e}^{\mathrm{x}} \mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}} \mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \\ $$$$\mathrm{Y}=\mathrm{y}_{\mathrm{gh}} +\mathrm{y}_{\mathrm{PI}} \\ $$$$\:\:\:\:=\alpha\mathrm{e}^{\mathrm{x}} +\beta\mathrm{e}^{−\mathrm{x}} −\mathrm{sin}\left(\mathrm{e}^{−\mathrm{x}} \right)−\mathrm{e}^{\mathrm{x}} \mathrm{cos}\left(\mathrm{e}^{−\mathrm{x}} \right) \\ $$

Facebook Tweet Pin