Question Number 135174 by bemath last updated on 11/Mar/21
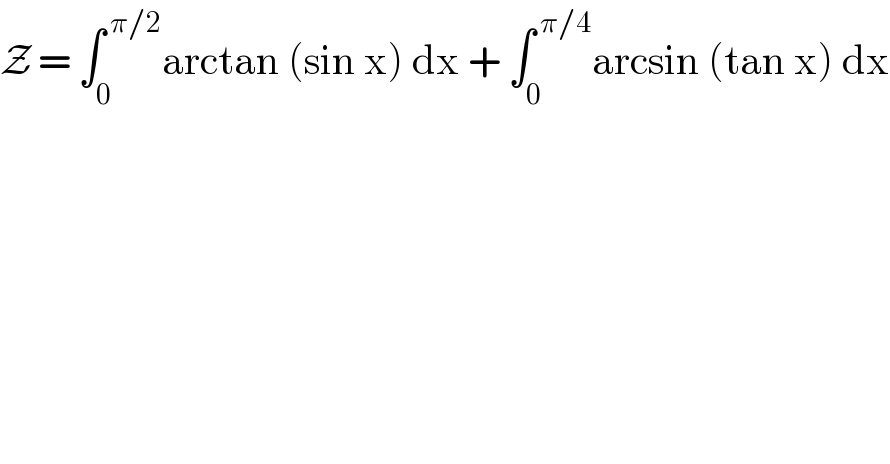
$$\mathcal{Z}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{arctan}\:\left(\mathrm{sin}\:\mathrm{x}\right)\:\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \mathrm{arcsin}\:\left(\mathrm{tan}\:\mathrm{x}\right)\:\mathrm{dx} \\ $$
Answered by john_santu last updated on 11/Mar/21
![let Z_1 =∫_0 ^( π/2) arctan (sin x)dx settng sin x = q ⇒Z_1 =∫_0 ^( 1) ((arctan (q))/( (√(1−q^2 )))) dq Z_1 = (arctan (q).arcsin (q)]_0 ^1 −∫_0 ^( 1) ((arcsin q)/(1+q^2 )) dq Z_1 = (π^2 /8)−∫_0 ^( 1) ((arcsin q)/(1+q^2 )) dq let Z_2 =∫_0 ^( π/4) arcsin (tan x)dx setting tan x = q Z_2 = ∫_0 ^( 1) ((arcsin (q))/(1+q^2 )) dq Now we get Z = Z_1 +Z_2 Z= (π^2 /8) −∫_0 ^( 1) ((arcsin (q))/(1+q^2 )) dq + ∫_0 ^( 1) ((arcsin (q))/(1+q^2 )) dq Z = (π^2 /8) •](https://www.tinkutara.com/question/Q135175.png)
$${let}\:\mathcal{Z}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{arctan}\:\left(\mathrm{sin}\:{x}\right){dx}\: \\ $$$${settng}\:\mathrm{sin}\:{x}\:=\:{q}\:\Rightarrow\mathcal{Z}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arctan}\:\left({q}\right)}{\:\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }}\:{dq} \\ $$$$\mathcal{Z}_{\mathrm{1}} =\:\left(\mathrm{arctan}\:\left({q}\right).\mathrm{arcsin}\:\left({q}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arcsin}\:{q}}{\mathrm{1}+{q}^{\mathrm{2}} }\:{dq} \\ $$$$\mathcal{Z}_{\mathrm{1}} =\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arcsin}\:{q}}{\mathrm{1}+{q}^{\mathrm{2}} }\:{dq} \\ $$$${let}\:\mathcal{Z}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \:\mathrm{arcsin}\:\left(\mathrm{tan}\:{x}\right){dx} \\ $$$${setting}\:\mathrm{tan}\:{x}\:=\:{q}\: \\ $$$$\mathcal{Z}_{\mathrm{2}} =\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arcsin}\:\left({q}\right)}{\mathrm{1}+{q}^{\mathrm{2}} }\:{dq}\: \\ $$$${Now}\:{we}\:{get}\:\mathcal{Z}\:=\:\mathcal{Z}_{\mathrm{1}} +\mathcal{Z}_{\mathrm{2}} \\ $$$$\mathcal{Z}=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arcsin}\:\left({q}\right)}{\mathrm{1}+{q}^{\mathrm{2}} }\:{dq}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{arcsin}\:\left({q}\right)}{\mathrm{1}+{q}^{\mathrm{2}} }\:{dq} \\ $$$$\mathcal{Z}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\bullet \\ $$
