Question Number 11355 by uni last updated on 21/Mar/17
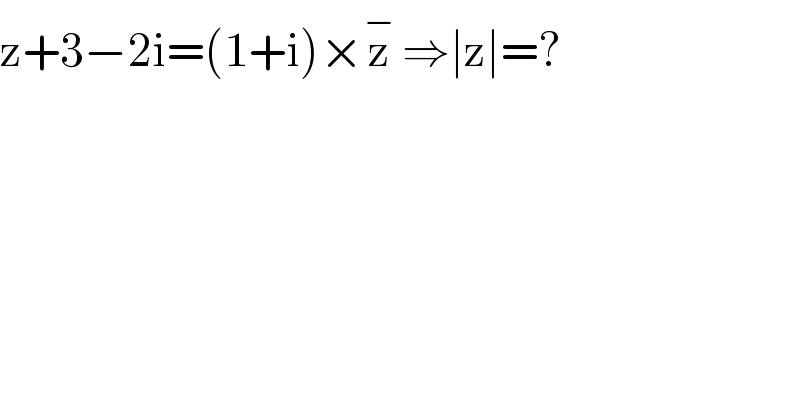
$$\mathrm{z}+\mathrm{3}−\mathrm{2i}=\left(\mathrm{1}+\mathrm{i}\right)×\overset{−} {\mathrm{z}}\:\Rightarrow\mid\mathrm{z}\mid=? \\ $$
Answered by sou1618 last updated on 22/Mar/17
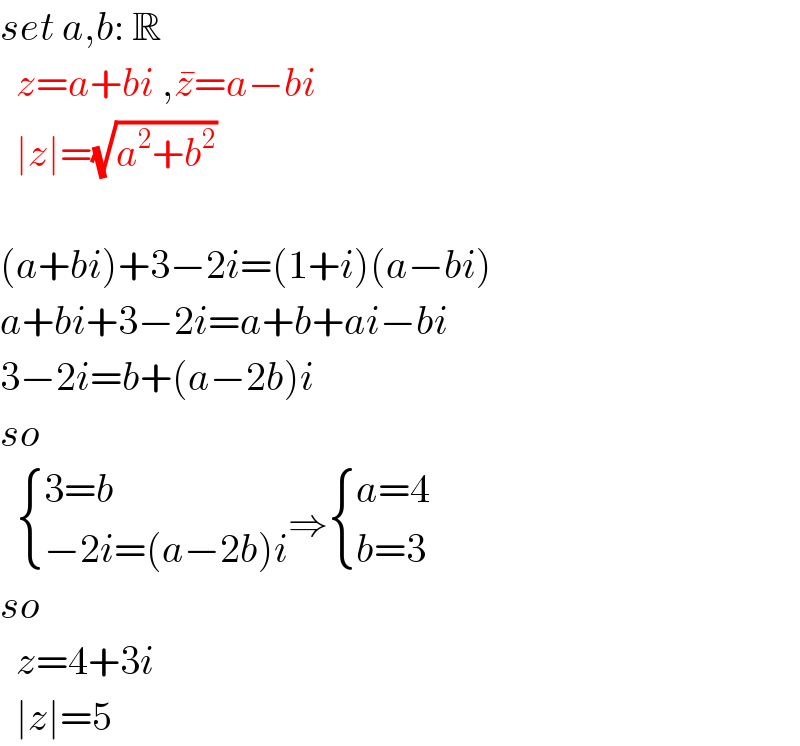
$${set}\:{a},{b}:\:\mathbb{R} \\ $$$$\:\:{z}={a}+{bi}\:,\bar {{z}}={a}−{bi} \\ $$$$\:\:\mid{z}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left({a}+{bi}\right)+\mathrm{3}−\mathrm{2}{i}=\left(\mathrm{1}+{i}\right)\left({a}−{bi}\right) \\ $$$${a}+{bi}+\mathrm{3}−\mathrm{2}{i}={a}+{b}+{ai}−{bi} \\ $$$$\mathrm{3}−\mathrm{2}{i}={b}+\left({a}−\mathrm{2}{b}\right){i} \\ $$$${so} \\ $$$$\:\:\begin{cases}{\mathrm{3}={b}}\\{−\mathrm{2}{i}=\left({a}−\mathrm{2}{b}\right){i}}\end{cases}\Rightarrow\begin{cases}{{a}=\mathrm{4}}\\{{b}=\mathrm{3}}\end{cases} \\ $$$${so} \\ $$$$\:\:{z}=\mathrm{4}+\mathrm{3}{i} \\ $$$$\:\:\mid{z}\mid=\mathrm{5} \\ $$
