Question Number 71564 by 20190927 last updated on 17/Oct/19

$$\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{4}} =−\mathrm{7}+\mathrm{24i} \\ $$
Commented by mathmax by abdo last updated on 18/Oct/19
![we have ∣−7+24i∣=(√(7^2 +24^2 ))=(√(49+576))=(√(625))=25 ⇒ −7+24i =25 e^(−iarctan(((24)/7))) and (z−i)^4 =25 e^(−iarctan(((24)/7))) let z−i=re^(iθ) ⇒r^4 e^(i4θ) =25 e^(−iarctan(((24)/7))) ⇒r=^4 (√(25))=(5^2 )^(1/4) =(√5) 4θ =−arctan(((24)/7))+2kπ ⇒θ_k =−((arctan(((24)/7)))/4) +((kπ)/2) and k∈[[0,3]] so the roots ofthis equations are Z_k =(√5)e^(i(((kπ)/2)−((arctan(((24)/7)))/4))) +i with 0≤k≤3](https://www.tinkutara.com/question/Q71661.png)
$${we}\:{have}\:\mid−\mathrm{7}+\mathrm{24}{i}\mid=\sqrt{\mathrm{7}^{\mathrm{2}} \:+\mathrm{24}^{\mathrm{2}} }=\sqrt{\mathrm{49}+\mathrm{576}}=\sqrt{\mathrm{625}}=\mathrm{25}\:\Rightarrow \\ $$$$−\mathrm{7}+\mathrm{24}{i}\:=\mathrm{25}\:{e}^{−{iarctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)} \:\:{and}\:\left({z}−{i}\right)^{\mathrm{4}} \:=\mathrm{25}\:{e}^{−{iarctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)} \:{let}\: \\ $$$${z}−{i}={re}^{{i}\theta} \:\Rightarrow{r}^{\mathrm{4}} {e}^{{i}\mathrm{4}\theta} =\mathrm{25}\:{e}^{−{iarctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)} \:\Rightarrow{r}=^{\mathrm{4}} \sqrt{\mathrm{25}}=\left(\mathrm{5}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\sqrt{\mathrm{5}} \\ $$$$\mathrm{4}\theta\:=−{arctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)+\mathrm{2}{k}\pi\:\Rightarrow\theta_{{k}} =−\frac{{arctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)}{\mathrm{4}}\:+\frac{{k}\pi}{\mathrm{2}} \\ $$$${and}\:{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right]\:{so}\:{the}\:{roots}\:{ofthis}\:{equations}\:{are} \\ $$$${Z}_{{k}} =\sqrt{\mathrm{5}}{e}^{{i}\left(\frac{{k}\pi}{\mathrm{2}}−\frac{{arctan}\left(\frac{\mathrm{24}}{\mathrm{7}}\right)}{\mathrm{4}}\right)} \:+{i}\:\:\:{with}\:\mathrm{0}\leqslant{k}\leqslant\mathrm{3} \\ $$$$ \\ $$$$ \\ $$
Commented by 20190927 last updated on 21/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by MJS last updated on 17/Oct/19
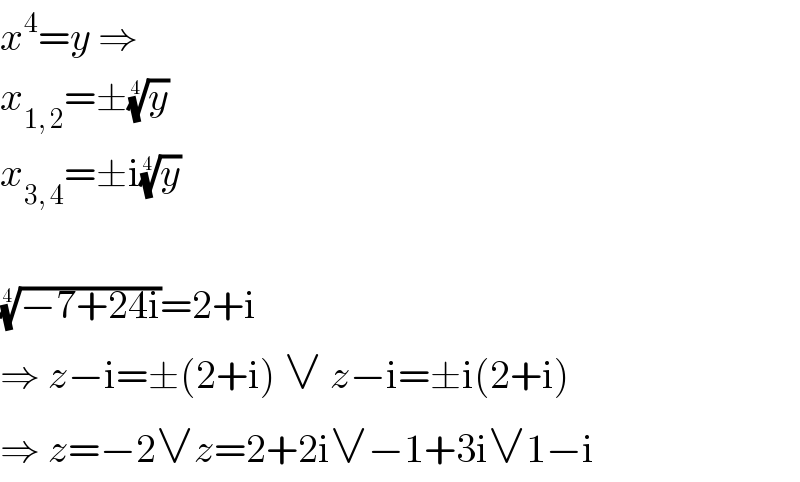
$${x}^{\mathrm{4}} ={y}\:\Rightarrow \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\pm\sqrt[{\mathrm{4}}]{{y}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =\pm\mathrm{i}\sqrt[{\mathrm{4}}]{{y}} \\ $$$$ \\ $$$$\sqrt[{\mathrm{4}}]{−\mathrm{7}+\mathrm{24i}}=\mathrm{2}+\mathrm{i} \\ $$$$\Rightarrow\:{z}−\mathrm{i}=\pm\left(\mathrm{2}+\mathrm{i}\right)\:\vee\:{z}−\mathrm{i}=\pm\mathrm{i}\left(\mathrm{2}+\mathrm{i}\right) \\ $$$$\Rightarrow\:{z}=−\mathrm{2}\vee{z}=\mathrm{2}+\mathrm{2i}\vee−\mathrm{1}+\mathrm{3i}\vee\mathrm{1}−\mathrm{i} \\ $$
Commented by 20190927 last updated on 21/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$$$ \\ $$
