Question Number 128110 by Dwaipayan Shikari last updated on 04/Jan/21
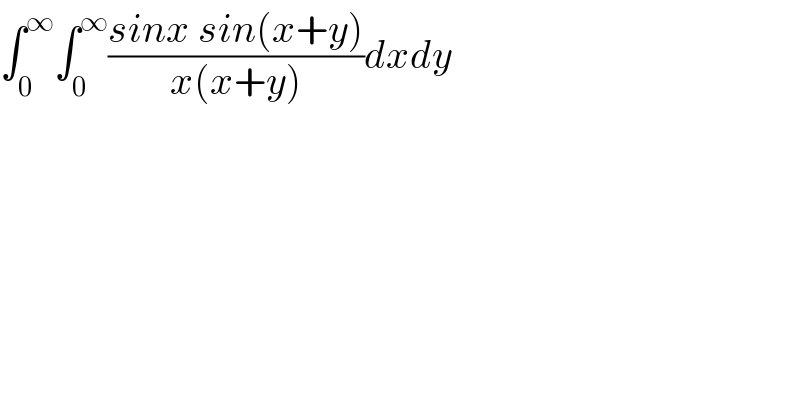
$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{sinx}\:{sin}\left({x}+{y}\right)}{{x}\left({x}+{y}\right)}{dxdy} \\ $$
Answered by Olaf last updated on 04/Jan/21
![Ω = ∫_0 ^∞ ∫_0 ^∞ ((sinxsin(x+y))/(x(x+y)))dxdy Ω = ∫_0 ^∞ ((sinx)/x)(∫_0 ^∞ ((sin(x+y))/(x+y))dy)dx Ω = ∫_0 ^∞ ((sinx)/x)(∫_x ^∞ ((sinu)/u)du)dx Ω = ∫_0 ^∞ ((sinx)/x)(∫_0 ^∞ ((sinu)/u)du−∫_0 ^x ((sinu)/u)du)dx Ω = ∫_0 ^∞ ((sinx)/x)((π/2)−Si(x))dx Ω = (π/2)∫_0 ^∞ ((sinx)/x)dx−∫_0 ^∞ ((sinx)/x)Si(x)dx Ω = (π^2 /4)−∫_0 ^∞ Si′(x)Si(x)dx Ω = (π^2 /4)−(1/2)[Si^2 (x)]_0 ^∞ Ω = (π^2 /4)−(1/2)(lim_(x→∞) Si(x))^2 Ω = (π^2 /4)−(1/2).(π^2 /4) Ω = (π^2 /8)](https://www.tinkutara.com/question/Q128134.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}\mathrm{sin}\left({x}+{y}\right)}{{x}\left({x}+{y}\right)}{dxdy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\left(\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({x}+{y}\right)}{{x}+{y}}{dy}\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\left(\int_{{x}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}}{du}\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\left(\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}}{du}−\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{sin}{u}}{{u}}{du}\right){dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{Si}\left({x}\right)\right){dx} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}{dx}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}\mathrm{Si}\left({x}\right){dx} \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\int_{\mathrm{0}} ^{\infty} \mathrm{Si}'\left({x}\right)\mathrm{Si}\left({x}\right){dx} \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{Si}^{\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{Si}\left({x}\right)\right)^{\mathrm{2}} \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by Dwaipayan Shikari last updated on 04/Jan/21

$${Great}\:{sir}\:! \\ $$
Commented by BHOOPENDRA last updated on 05/Jan/21

$${great}\:{sir} \\ $$
