Question Number 113816 by Study last updated on 15/Sep/20
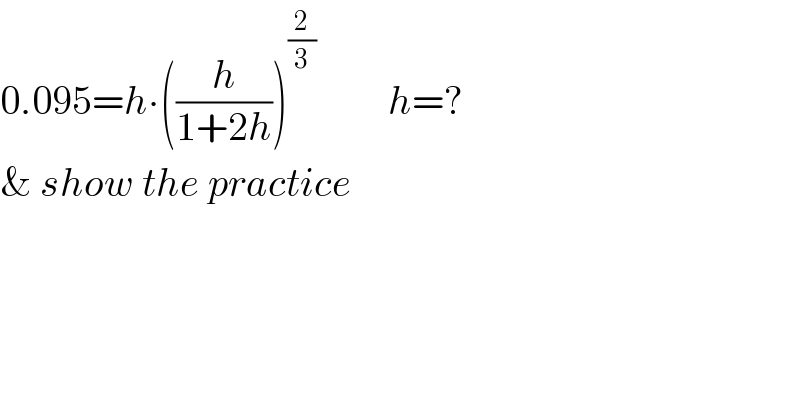
$$\mathrm{0}.\mathrm{095}={h}\centerdot\left(\frac{{h}}{\mathrm{1}+\mathrm{2}{h}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\:\:\:\:\:\:\:\:{h}=?\:\: \\ $$$$\&\:{show}\:{the}\:{practice} \\ $$
Commented by Study last updated on 15/Sep/20
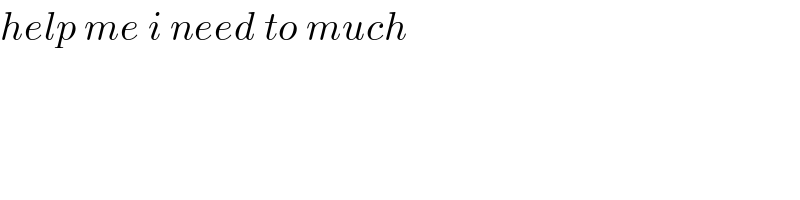
$${help}\:{me}\:{i}\:{need}\:{to}\:{much} \\ $$
Answered by MJS_new last updated on 15/Sep/20
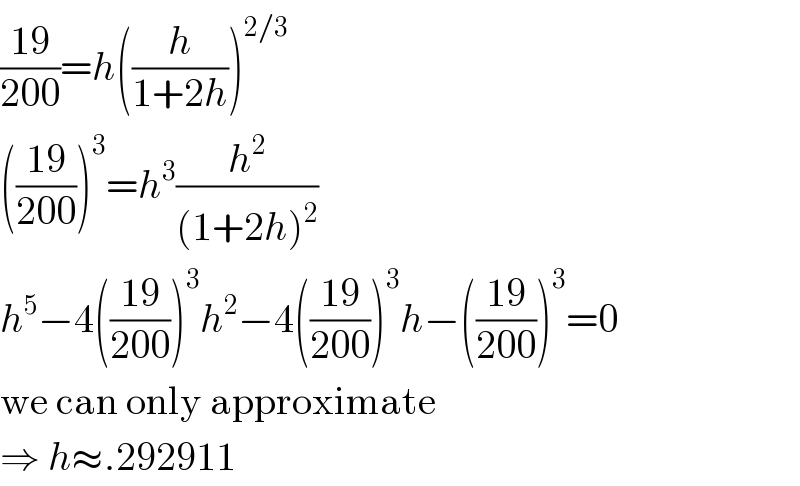
$$\frac{\mathrm{19}}{\mathrm{200}}={h}\left(\frac{{h}}{\mathrm{1}+\mathrm{2}{h}}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\left(\frac{\mathrm{19}}{\mathrm{200}}\right)^{\mathrm{3}} ={h}^{\mathrm{3}} \frac{{h}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{2}{h}\right)^{\mathrm{2}} } \\ $$$${h}^{\mathrm{5}} −\mathrm{4}\left(\frac{\mathrm{19}}{\mathrm{200}}\right)^{\mathrm{3}} {h}^{\mathrm{2}} −\mathrm{4}\left(\frac{\mathrm{19}}{\mathrm{200}}\right)^{\mathrm{3}} {h}−\left(\frac{\mathrm{19}}{\mathrm{200}}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate} \\ $$$$\Rightarrow\:{h}\approx.\mathrm{292911} \\ $$
