Question Number 152703 by talminator2856791 last updated on 31/Aug/21
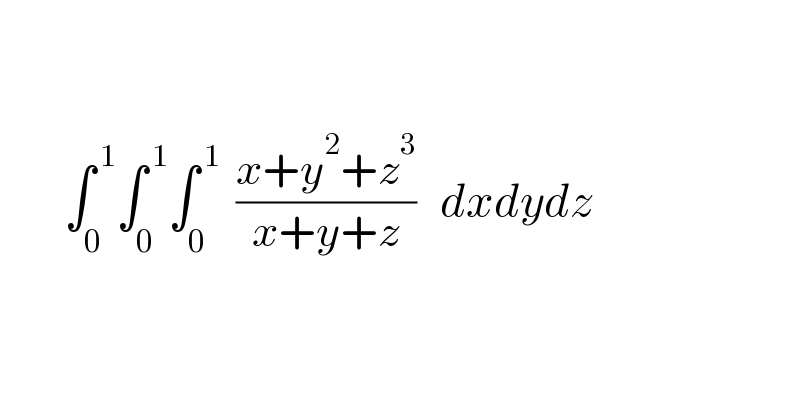
$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \:\:\frac{{x}+{y}^{\mathrm{2}} +{z}^{\mathrm{3}} }{{x}+{y}+{z}}\:\:\:{dxdydz} \\ $$$$\: \\ $$$$\: \\ $$
Answered by Jamshidbek last updated on 31/Aug/21
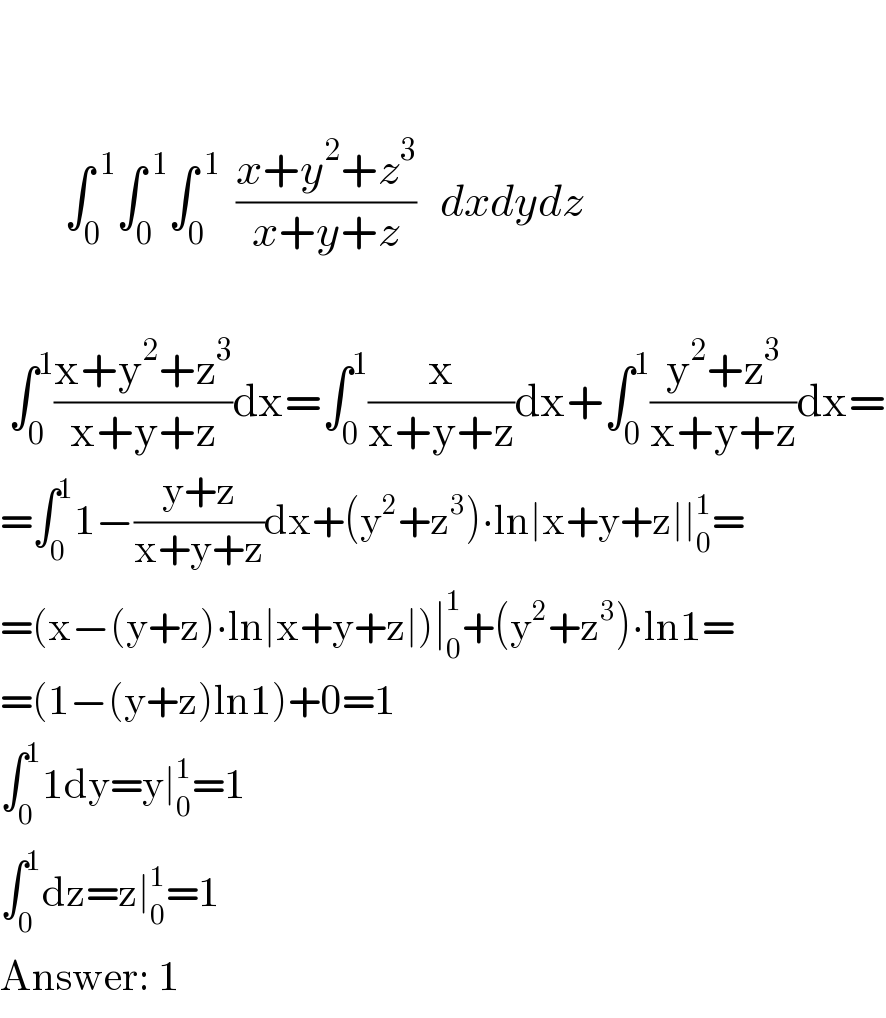
$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \:\:\frac{{x}+{y}^{\mathrm{2}} +{z}^{\mathrm{3}} }{{x}+{y}+{z}}\:\:\:{dxdydz} \\ $$$$\: \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}+\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{3}} }{\mathrm{x}+\mathrm{y}+\mathrm{z}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\mathrm{x}+\mathrm{y}+\mathrm{z}}\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{3}} }{\mathrm{x}+\mathrm{y}+\mathrm{z}}\mathrm{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}−\frac{\mathrm{y}+\mathrm{z}}{\mathrm{x}+\mathrm{y}+\mathrm{z}}\mathrm{dx}+\left(\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{3}} \right)\centerdot\mathrm{ln}\mid\mathrm{x}+\mathrm{y}+\mathrm{z}\mid\mid_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\left(\mathrm{x}−\left(\mathrm{y}+\mathrm{z}\right)\centerdot\mathrm{ln}\mid\mathrm{x}+\mathrm{y}+\mathrm{z}\mid\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\left(\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{3}} \right)\centerdot\mathrm{ln1}= \\ $$$$=\left(\mathrm{1}−\left(\mathrm{y}+\mathrm{z}\right)\mathrm{ln1}\right)+\mathrm{0}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1dy}=\mathrm{y}\mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{dz}=\mathrm{z}\mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{Answer}:\:\mathrm{1} \\ $$
Commented by Olaf_Thorendsen last updated on 31/Aug/21
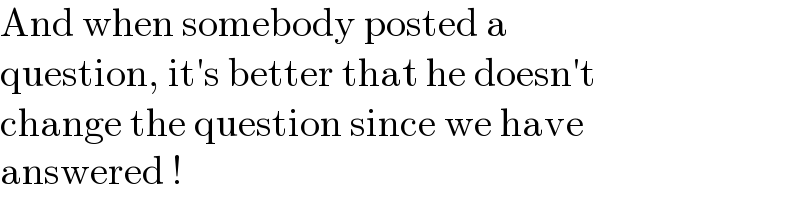
$$\mathrm{And}\:\mathrm{when}\:\mathrm{somebody}\:\mathrm{posted}\:\mathrm{a} \\ $$$$\mathrm{question},\:\mathrm{it}'\mathrm{s}\:\mathrm{better}\:\mathrm{that}\:\mathrm{he}\:\mathrm{doesn}'\mathrm{t} \\ $$$$\mathrm{change}\:\mathrm{the}\:\mathrm{question}\:\mathrm{since}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{answered}\:! \\ $$
Answered by Olaf_Thorendsen last updated on 31/Aug/21

$$\mathrm{Are}\:\mathrm{you}\:\mathrm{sure}\:\mathrm{this}\:\mathrm{is}\:\mathrm{really}\:\mathrm{your} \\ $$$$\mathrm{question}\:\mathrm{or}\:\mathrm{you}\:\mathrm{will}\:\mathrm{change}\:\mathrm{a}\:\mathrm{new} \\ $$$$\mathrm{time}\:? \\ $$
Commented by SANOGO last updated on 31/Aug/21
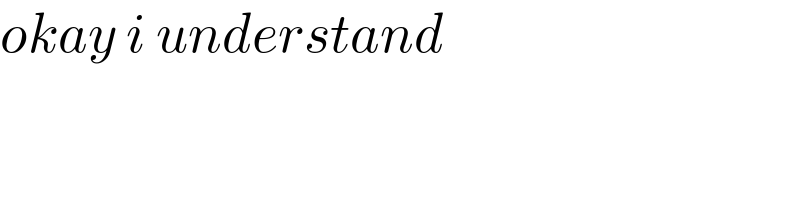
$${okay}\:{i}\:{understand} \\ $$
