Question Number 128057 by bramlexs22 last updated on 04/Jan/21
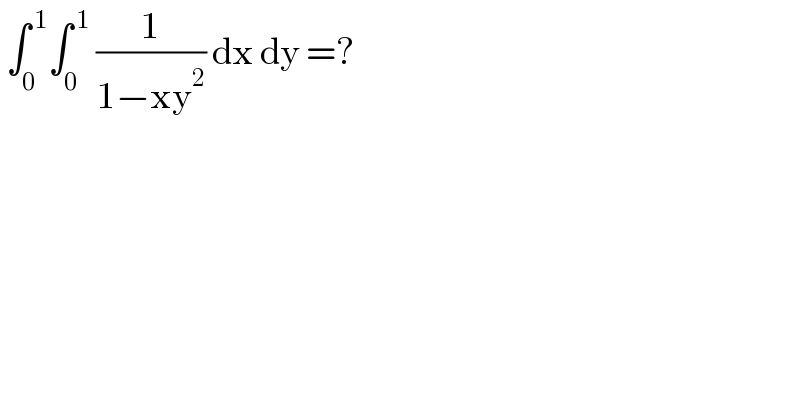
$$\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\:\mathrm{dx}\:\mathrm{dy}\:=? \\ $$
Answered by liberty last updated on 04/Jan/21
![(1/(1−xy^2 )) = Σ_(m=0) ^∞ (xy^2 )^m I=∫_0 ^( 1) ∫_0 ^( 1) (1/(1−xy^2 )) dx dy = Σ_(m=0) ^∞ ∫_0 ^( 1) x^m dx ∫_0 ^( 1) y^(2m) dy = Σ_(m=0) ^∞ (x^(m+1) /(m+1)) ]_0 ^1 . (y^(2m+1) /(2m+1)) ]_0 ^1 = Σ_(m=0) ^∞ (1/((m+1)(2m+1))) = Σ_(k=1) ^∞ (1/(k(2k−1))) ; k=m+1 = 2Σ_(k=1) ^∞ ((1/(2k−1)) −(1/(2k))) = 2Σ_(i=1) ^∞ (((−1)^(i−1) )/i) = 2 ln (2)](https://www.tinkutara.com/question/Q128059.png)
$$\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\:=\:\underset{\mathrm{m}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{m}} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\:\mathrm{dx}\:\mathrm{dy}\:=\:\underset{\mathrm{m}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{m}} \:\mathrm{dx}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{y}^{\mathrm{2m}} \:\mathrm{dy} \\ $$$$\left.\:\left.=\:\underset{\mathrm{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{x}^{\mathrm{m}+\mathrm{1}} }{\mathrm{m}+\mathrm{1}}\:\right]_{\mathrm{0}} ^{\mathrm{1}} \:.\:\frac{\mathrm{y}^{\mathrm{2m}+\mathrm{1}} }{\mathrm{2m}+\mathrm{1}}\:\right]_{\mathrm{0}} ^{\mathrm{1}} \: \\ $$$$\:=\:\underset{\mathrm{m}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{m}+\mathrm{1}\right)\left(\mathrm{2m}+\mathrm{1}\right)}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{2k}−\mathrm{1}\right)}\:;\:\mathrm{k}=\mathrm{m}+\mathrm{1} \\ $$$$\:=\:\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2k}}\right)\:=\:\mathrm{2}\underset{\mathrm{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{i}−\mathrm{1}} }{\mathrm{i}} \\ $$$$\:=\:\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$
Answered by Olaf last updated on 04/Jan/21
![Ω = ∫_0 ^1 ∫_0 ^1 ((dxdy)/(1−xy^2 )) Ω = ∫_0 ^1 (1/(2(√x)))∫_0 ^1 [((√x)/(1+(√x)y))+((√x)/(1−(√x)y))]dydx Ω = ∫_0 ^1 (1/(2(√x)))[ln(((1+(√x)y)/(1−(√x)y)))]_0 ^1 dx Ω = ∫_0 ^1 ((ln(((1+(√x))/(1−(√x)))))/(2(√x)))dx Ω = ∫_0 ^1 ln(((1+u)/(1−u)))du Ω = [(1+u)ln(1+u)+(1−u)ln(1−u)]_0 ^1 Ω = 2ln2](https://www.tinkutara.com/question/Q128061.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dxdy}}{\mathrm{1}−{xy}^{\mathrm{2}} } \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\sqrt{{x}}}{\mathrm{1}+\sqrt{{x}}{y}}+\frac{\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}{y}}\right]{dydx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\left[\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}{y}}{\mathrm{1}−\sqrt{{x}}{y}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} {dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\right)}{\mathrm{2}\sqrt{{x}}}{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\right){du} \\ $$$$\Omega\:=\:\left[\left(\mathrm{1}+{u}\right)\mathrm{ln}\left(\mathrm{1}+{u}\right)+\left(\mathrm{1}−{u}\right)\mathrm{ln}\left(\mathrm{1}−{u}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\mathrm{2ln2} \\ $$
Answered by mathmax by abdo last updated on 04/Jan/21
![∫_0 ^1 ∫_0 ^1 (1/(1−xy^2 ))dxdy =∫_0 ^1 (∫_0 ^(1 ) (dy/(1−xy^2 )))dx we have ∫_0 ^1 (dy/(1−xy^2 )) =∫_0 ^1 ((xy)/((1−(√x)y)(1+(√x)y)))=(1/2)∫_0 ^1 ((1/(1−(√x)y))+(1/(1+(√x)y)))dy =−(1/(2(√x)))[ln∣1−(√x)y∣]_(y=0) ^1 +(1/(2(√x)))[ln∣1+(√x)y∣]_(y=0) ^1 =(1/(2(√x)))ln(1+(√x))−(1/(2(√x)))ln(1−(√x)) =(1/(2(√x)))ln(((1+(√x))/(1−(√x)))) ⇒ I =(1/2)∫_0 ^1 (1/( (√x)))ln(((1+(√x))/(1−(√x))))dx =_((√x)=t) (1/2)∫_0 ^1 (1/t)ln(((1+t)/(1−t)))(2t)dt =∫_0 ^1 ln(1+t)dt(→1+t=u)−∫_0 ^1 ln(1−t)dt(→1−t=v) =∫_1 ^2 lnu du−∫_1 ^0 lnv(−dv) =∫_1 ^2 lnu du−∫_0 ^1 lnv dv =[ulnu−u]_1 ^2 −[vlnv−v]_0 ^1 =2ln2−2+1−(−1) =2ln2−2+2 ⇒I =2ln(2)](https://www.tinkutara.com/question/Q128085.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\mathrm{dxdy}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{\mathrm{dy}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\right)\mathrm{dx}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dy}}{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xy}}{\left(\mathrm{1}−\sqrt{\mathrm{x}}\mathrm{y}\right)\left(\mathrm{1}+\sqrt{\mathrm{x}}\mathrm{y}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\mathrm{x}}\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{x}}\mathrm{y}}\right)\mathrm{dy} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\left[\mathrm{ln}\mid\mathrm{1}−\sqrt{\mathrm{x}}\mathrm{y}\mid\right]_{\mathrm{y}=\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\left[\mathrm{ln}\mid\mathrm{1}+\sqrt{\mathrm{x}}\mathrm{y}\mid\right]_{\mathrm{y}=\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\mathrm{ln}\left(\mathrm{1}−\sqrt{\mathrm{x}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{x}}}{\mathrm{1}−\sqrt{\mathrm{x}}}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{x}}}{\mathrm{1}−\sqrt{\mathrm{x}}}\right)\mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{t}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\right)\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)\mathrm{dt}\left(\rightarrow\mathrm{1}+\mathrm{t}=\mathrm{u}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\mathrm{dt}\left(\rightarrow\mathrm{1}−\mathrm{t}=\mathrm{v}\right) \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{lnu}\:\mathrm{du}−\int_{\mathrm{1}} ^{\mathrm{0}} \:\mathrm{lnv}\left(−\mathrm{dv}\right)\:=\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{lnu}\:\mathrm{du}−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lnv}\:\mathrm{dv} \\ $$$$=\left[\mathrm{ulnu}−\mathrm{u}\right]_{\mathrm{1}} ^{\mathrm{2}} \:−\left[\mathrm{vlnv}−\mathrm{v}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{2ln2}−\mathrm{2}+\mathrm{1}−\left(−\mathrm{1}\right)\:=\mathrm{2ln2}−\mathrm{2}+\mathrm{2} \\ $$$$\Rightarrow\mathrm{I}\:=\mathrm{2ln}\left(\mathrm{2}\right) \\ $$
