Question Number 128175 by bemath last updated on 05/Jan/21
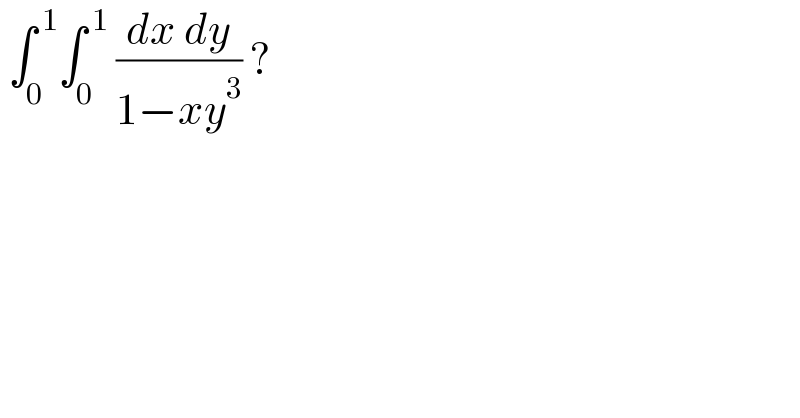
$$\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{dx}\:{dy}}{\mathrm{1}−{xy}^{\mathrm{3}} }\:? \\ $$
Commented by liberty last updated on 06/Jan/21
![(1/(1−xy^3 )) = Σ_(n=0) ^∞ (xy^3 )^n I=Σ_(n=0) ^∞ ∫_0 ^( 1) ∫_0 ^( 1) (xy^3 )^n dy dx = Σ_(n=0) ^∞ ∫_0 ^( 1) x^n dx.∫_0 ^( 1) y^(3n) dy = Σ_(n=0) ^∞ (x^(n+1) /(n+1)) ∣_0 ^1 . (y^(3n+1) /(3n+1)) ∣_0 ^1 = Σ_(n=0) ^∞ (1/((n+1)(3n+1))) = (3/2)Σ_(n=0) ^∞ ((1/(3n+1))−(1/(3n+3))) = (3/2)Σ_(n=0) ^∞ ∫_0 ^( 1) (x^(3n) −x^(3n+2) ) dx = (3/2)∫_0 ^( 1) ((1−x^2 )/(1−x^3 )) dx = (3/2)∫_0 ^( 1) ((1+x)/(1+x+x^2 )) dx = (3/2)∫_0 ^( 1) ((x+(1/2))/((x+(1/2))^2 +(3/4)))+(3/4)∫_0 ^( 1) (1/((x+(1/2))^2 +(3/4))) dx = [(3/2).(1/2)ln ((x+(1/2))^2 +(3/4))+(3/4).(2/( (√3))) tan^(−1) (((x+(1/2))/((√3)/2))) ]_0 ^1 = (1/(12)) (π(√3) + 9 ln 3)](https://www.tinkutara.com/question/Q128284.png)
$$\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}^{\mathrm{3}} }\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(\mathrm{xy}^{\mathrm{3}} \right)^{\mathrm{n}} \: \\ $$$$\mathrm{I}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{xy}^{\mathrm{3}} \right)^{\mathrm{n}} \:\mathrm{dy}\:\mathrm{dx}\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{n}} \:\mathrm{dx}.\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{y}^{\mathrm{3n}} \:\mathrm{dy} \\ $$$$\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:\mid_{\mathrm{0}} ^{\mathrm{1}} .\:\frac{\mathrm{y}^{\mathrm{3n}+\mathrm{1}} }{\mathrm{3n}+\mathrm{1}}\:\mid_{\mathrm{0}} ^{\mathrm{1}} =\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{3n}+\mathrm{1}\right)} \\ $$$$\:=\:\frac{\mathrm{3}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{3n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3n}+\mathrm{3}}\right) \\ $$$$\:=\:\frac{\mathrm{3}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{x}^{\mathrm{3n}} −\mathrm{x}^{\mathrm{3n}+\mathrm{2}} \right)\:\mathrm{dx}\: \\ $$$$\:=\:\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{3}} }\:\mathrm{dx}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\:=\:\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\:\mathrm{dx} \\ $$$$\:=\:\left[\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)+\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{12}}\:\left(\pi\sqrt{\mathrm{3}}\:+\:\mathrm{9}\:\mathrm{ln}\:\mathrm{3}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jan/21
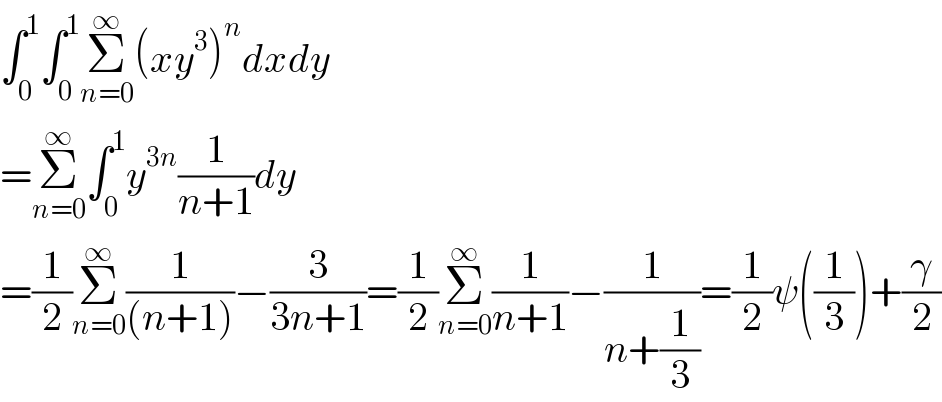
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({xy}^{\mathrm{3}} \right)^{{n}} {dxdy} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\mathrm{3}{n}} \frac{\mathrm{1}}{{n}+\mathrm{1}}{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{3}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\gamma}{\mathrm{2}} \\ $$
