Question Number 189549 by mnjuly1970 last updated on 18/Mar/23

$$ \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{dxdy}}{\left(\mathrm{1}+{xy}\:\right)^{\:\mathrm{4}} }=? \\ $$
Answered by witcher3 last updated on 18/Mar/23
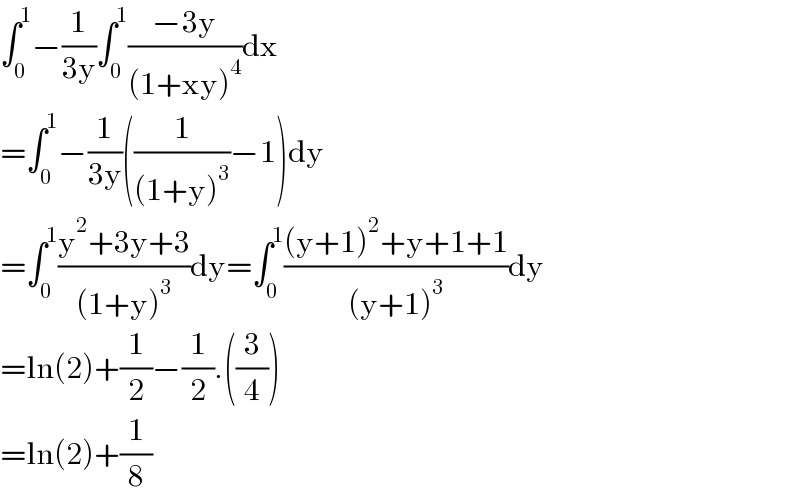
$$\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{3y}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{3y}}{\left(\mathrm{1}+\mathrm{xy}\right)^{\mathrm{4}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{3y}}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{y}\right)^{\mathrm{3}} }−\mathrm{1}\right)\mathrm{dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{y}^{\mathrm{2}} +\mathrm{3y}+\mathrm{3}}{\left(\mathrm{1}+\mathrm{y}\right)^{\mathrm{3}} }\mathrm{dy}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{y}+\mathrm{1}+\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dy} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}.\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{8}} \\ $$
