Question Number 63292 by aliesam last updated on 02/Jul/19
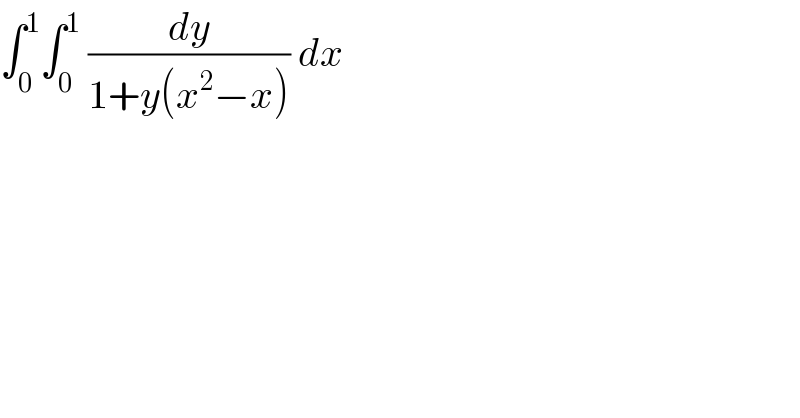
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dy}}{\mathrm{1}+{y}\left({x}^{\mathrm{2}} −{x}\right)}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19
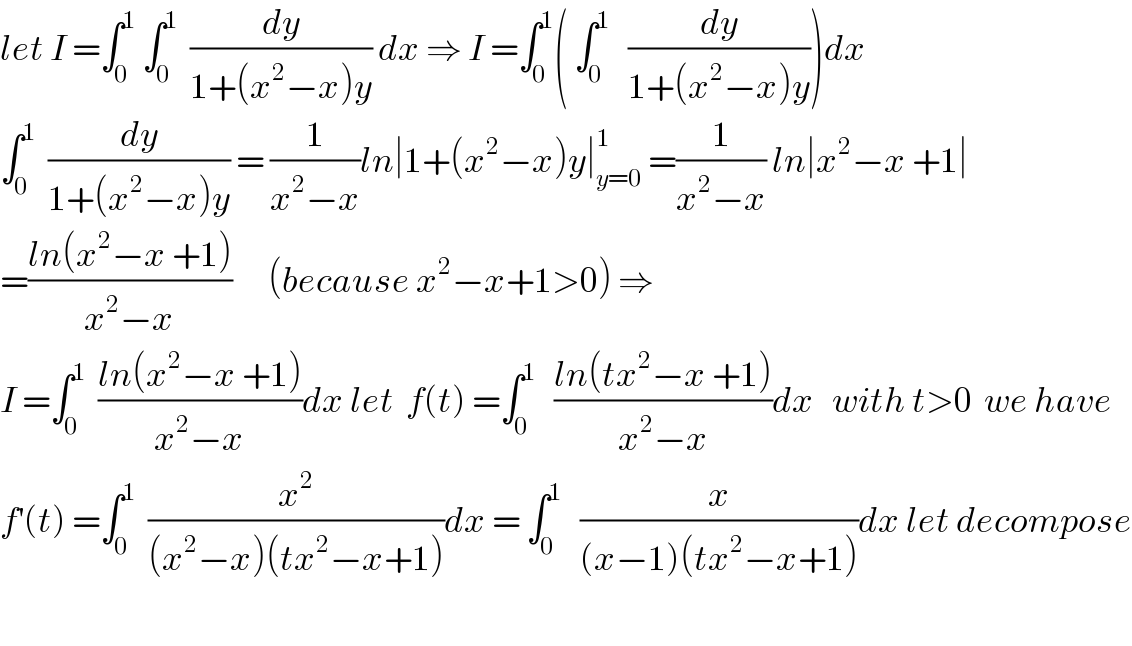
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dy}}{\mathrm{1}+\left({x}^{\mathrm{2}} −{x}\right){y}}\:{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dy}}{\mathrm{1}+\left({x}^{\mathrm{2}} −{x}\right){y}}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dy}}{\mathrm{1}+\left({x}^{\mathrm{2}} −{x}\right){y}}\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}}{ln}\mid\mathrm{1}+\left({x}^{\mathrm{2}} −{x}\right){y}\mid_{{y}=\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}}\:{ln}\mid{x}^{\mathrm{2}} −{x}\:+\mathrm{1}\mid \\ $$$$=\frac{{ln}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}}\:\:\:\:\:\:\left({because}\:{x}^{\mathrm{2}} −{x}+\mathrm{1}>\mathrm{0}\right)\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}}{dx}\:{let}\:\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left({tx}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}}{dx}\:\:\:{with}\:{t}>\mathrm{0}\:\:{we}\:{have} \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{x}\right)\left({tx}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}}{\left({x}−\mathrm{1}\right)\left({tx}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx}\:{let}\:{decompose} \\ $$$$ \\ $$
Commented by aliesam last updated on 02/Jul/19

$${nice}\:{solution}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19
![let decompose F(x)=(x/((x−1)(tx^2 −x +1))) F(x)=(a/(x−1)) +((bx +c)/(tx^2 −x+1)) a =lim_(x→1) (x−1)F(x) = (1/t) lim_(x→+∞) xF(x) =0 = a+(b/t) ⇒at +b =0 ⇒b =−at =−1 ⇒ F(x) = (1/(t(x−1))) +((−x +c)/(tx^2 −x +1)) F(2) =(2/(4t−1)) =(1/t) +((−2+c)/(4t−1)) ⇒2 =((4t−1)/t) −2 +c ⇒c=4−((4t−1)/t) =(1/t) ⇒ F(t) =(1/(t(x−1))) +((−x+(1/t))/(tx^2 −x+1)) =(1/(t(x−1))) +((−tx +1)/(t(tx^2 −x+1))) ⇒ f^′ (t) =∫_0 ^1 (1/(t(x−1)))dx −(1/t) ∫_0 ^1 ((tx−1)/(tx^2 −x+1))dx =(1/t){∫_0 ^1 (dx/(x−1)) −(1/2)∫_0 ^1 ((2tx−1−1)/(tx^2 −x+1))dx} =(1/t) { [ln∣x−1∣ −(1/2)ln(tx^2 −x+1)]_(x=0) ^1 +(1/2) ∫_0 ^1 (dx/(tx^2 −x+1))} =(1/t){[ ln(((∣x−1∣)/( (√(tx^2 −x+1)))))]_(x=0) ^1 +(1/2) ∫_0 ^1 (dx/(tx^2 −x+1))}....perhaps the integral diverges... ...be continued....](https://www.tinkutara.com/question/Q63348.png)
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{{x}}{\left({x}−\mathrm{1}\right)\left({tx}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{bx}\:+{c}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{1}} \:\left({x}−\mathrm{1}\right){F}\left({x}\right)\:=\:\frac{\mathrm{1}}{{t}} \\ $$$${lim}_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)\:=\mathrm{0}\:=\:{a}+\frac{{b}}{{t}}\:\Rightarrow{at}\:+{b}\:=\mathrm{0}\:\Rightarrow{b}\:=−{at}\:=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{{t}\left({x}−\mathrm{1}\right)}\:+\frac{−{x}\:+{c}}{{tx}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{2}\right)\:=\frac{\mathrm{2}}{\mathrm{4}{t}−\mathrm{1}}\:=\frac{\mathrm{1}}{{t}}\:+\frac{−\mathrm{2}+{c}}{\mathrm{4}{t}−\mathrm{1}}\:\Rightarrow\mathrm{2}\:=\frac{\mathrm{4}{t}−\mathrm{1}}{{t}}\:−\mathrm{2}\:+{c}\:\Rightarrow{c}=\mathrm{4}−\frac{\mathrm{4}{t}−\mathrm{1}}{{t}}\:=\frac{\mathrm{1}}{{t}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}\left({x}−\mathrm{1}\right)}\:+\frac{−{x}+\frac{\mathrm{1}}{{t}}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{{t}\left({x}−\mathrm{1}\right)}\:+\frac{−{tx}\:+\mathrm{1}}{{t}\left({tx}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{t}\left({x}−\mathrm{1}\right)}{dx}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{tx}−\mathrm{1}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{{t}}\left\{\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{tx}−\mathrm{1}−\mathrm{1}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\right\} \\ $$$$=\frac{\mathrm{1}}{{t}}\:\left\{\:\left[{ln}\mid{x}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({tx}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right]_{{x}=\mathrm{0}} ^{\mathrm{1}} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{{t}}\left\{\left[\:\:{ln}\left(\frac{\mid{x}−\mathrm{1}\mid}{\:\sqrt{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}}\right)\right]_{{x}=\mathrm{0}} ^{\mathrm{1}} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{{tx}^{\mathrm{2}} −{x}+\mathrm{1}}\right\}….{perhaps}\:{the}\:{integral}\:{diverges}… \\ $$$$…{be}\:{continued}…. \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19
![let change the ordre of integral I =∫_0 ^1 (∫_0 ^1 (dx/(1+yx^2 −yx)))dy we have A(y)=∫_0 ^1 (dx/(yx^2 −yx +1)) →let solve yx^2 −yx +1 =0 Δ =y^2 −4y <0 due to 0≤y≤1 ⇒yx^2 −yx +1=y(x^2 −x +(1/y)) =y( x^2 −2x(1/2) +(1/4) +(1/y) −(1/4)) =y{ (x−(1/2))^2 +((4−y)/y)} ( y≠0) we use the changement x−(1/2) =(√((4−y)/y))t ⇒t =((2x−1)/2) (√(y/(4−y))) A(y) = ∫_(−(1/2)(√(y/(4−y)))) ^((1/2)(√(y/(4−y)))) (1/(y ((4−y)/y)(1+t^2 ))) (√((4−y)/y))dt =(1/( (√(y(4−y))))) [arctan(t)]_(−(1/2)(√(y/(4−y)))) ^((1/2)(√(y/(4−y)))) =((2arctan((1/2)(√(y/(4−y)))))/( (√(y(4−y))))) ⇒ I =2 ∫_0 ^1 ((arctan((1/2)(√(y/(4−y)))))/( (√(y(4−y))))) dy ....be continued....](https://www.tinkutara.com/question/Q63350.png)
$${let}\:{change}\:{the}\:{ordre}\:{of}\:{integral} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{yx}^{\mathrm{2}} −{yx}}\right){dy}\:\:{we}\:{have} \\ $$$${A}\left({y}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{yx}^{\mathrm{2}} −{yx}\:+\mathrm{1}}\:\rightarrow{let}\:{solve}\:{yx}^{\mathrm{2}} −{yx}\:+\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:={y}^{\mathrm{2}} −\mathrm{4}{y}\:<\mathrm{0}\:\:{due}\:{to}\:\:\mathrm{0}\leqslant{y}\leqslant\mathrm{1}\:\Rightarrow{yx}^{\mathrm{2}} −{yx}\:+\mathrm{1}={y}\left({x}^{\mathrm{2}} −{x}\:+\frac{\mathrm{1}}{{y}}\right) \\ $$$$={y}\left(\:{x}^{\mathrm{2}} −\mathrm{2}{x}\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{{y}}\:−\frac{\mathrm{1}}{\mathrm{4}}\right)\:={y}\left\{\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}−{y}}{{y}}\right\}\:\:\:\:\left(\:{y}\neq\mathrm{0}\right) \\ $$$${we}\:{use}\:{the}\:{changement}\:\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\sqrt{\frac{\mathrm{4}−{y}}{{y}}}{t}\:\Rightarrow{t}\:=\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}}\:\sqrt{\frac{{y}}{\mathrm{4}−{y}}} \\ $$$${A}\left({y}\right)\:=\:\int_{−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}} ^{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}} \:\:\:\:\:\frac{\mathrm{1}}{{y}\:\frac{\mathrm{4}−{y}}{{y}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\sqrt{\frac{\mathrm{4}−{y}}{{y}}}{dt} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{y}\left(\mathrm{4}−{y}\right)}}\:\left[{arctan}\left({t}\right)\right]_{−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}} ^{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}} \:\:=\frac{\mathrm{2}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}\right)}{\:\sqrt{{y}\left(\mathrm{4}−{y}\right)}}\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{y}}{\mathrm{4}−{y}}}\right)}{\:\sqrt{{y}\left(\mathrm{4}−{y}\right)}}\:{dy}\:\:\:\:….{be}\:{continued}…. \\ $$
