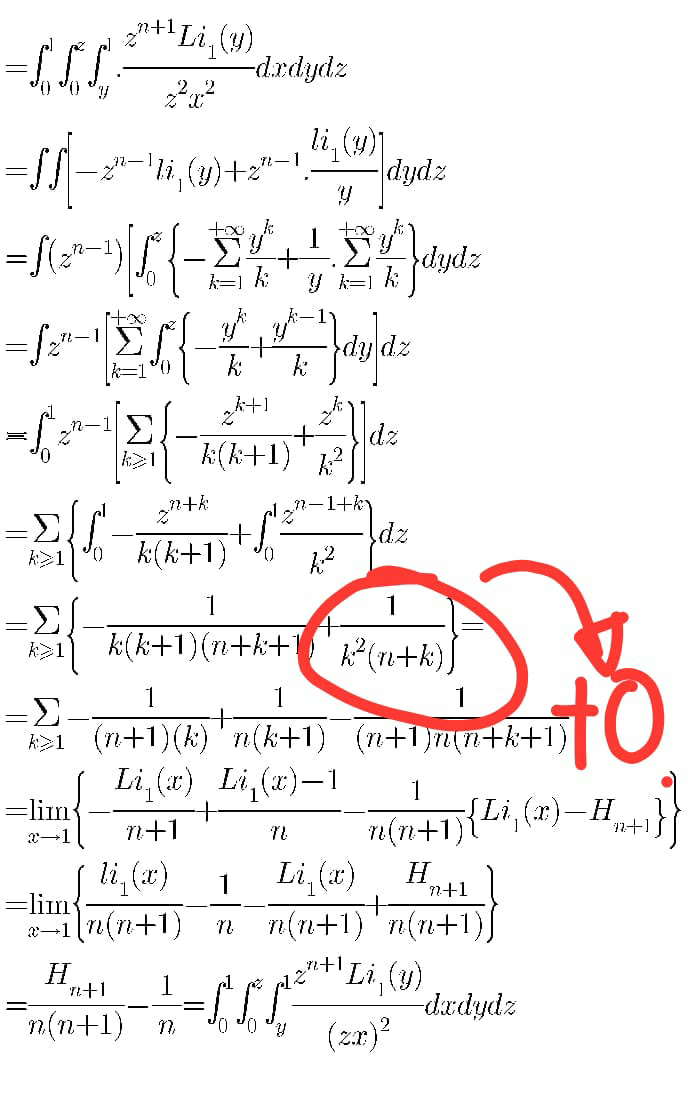Question Number 83342 by M±th+et£s last updated on 01/Mar/20
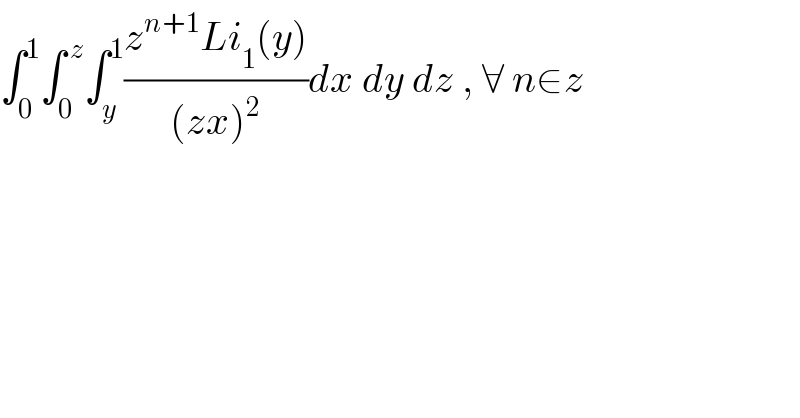
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\:{z}} \int_{{y}} ^{\mathrm{1}} \frac{{z}^{{n}+\mathrm{1}} {Li}_{\mathrm{1}} \left({y}\right)}{\left({zx}\right)^{\mathrm{2}} }{dx}\:{dy}\:{dz}\:,\:\forall\:{n}\in{z} \\ $$
Answered by mind is power last updated on 01/Mar/20
![=∫_0 ^1 ∫_0 ^z ∫_y ^1 .((z^(n+1) Li_1 (y))/(z^2 x^2 ))dxdydz =∫∫[−z^(n−1) li_1 (y)+z^(n−1) .((li_1 (y))/y)]dydz =∫(z^(n−1) )[∫_(0 ) ^z {−Σ_(k=1) ^(+∞) (y^k /k)+(1/y).Σ_(k=1) ^(+∞) (y^k /k)}dydz =∫z^(n−1) [Σ_(k=1) ^(+∞) ∫_0 ^z {−(y^k /k)+(y^(k−1) /k)}dy]dz =∫_0 ^1 z^(n−1) [Σ_(k≥1) {−(z^(k+1) /(k(k+1)))+(z^k /k^2 )}]dz =Σ_(k≥1) {∫_0 ^1 −(z^(n+k) /(k(k+1)))+∫_0 ^1 (z^(n−1+k) /k^2 )}dz =Σ_(k≥1) {−(1/(k(k+1)(n+k+1)))+(1/(k^2 (n+k)))}= =Σ_(k≥1) −(1/((n+1)(k)))+(1/(n(k+1)))−(1/((n+1)n(n+k+1))) =lim_(x→1) {−((Li_1 (x))/(n+1))+((Li_1 (x)−1)/n)−(1/(n(n+1))){Li_1 (x)−H_(n+1) }} =lim_(x→1) {((li_1 (x))/(n(n+1)))−(1/n)−((Li_1 (x))/(n(n+1)))+(H_(n+1) /(n(n+1)))} =(H_(n+1) /(n(n+1)))−(1/n)=∫_0 ^1 ∫_0 ^z ∫_y ^1 ((z^(n+1) Li_1 (y))/((zx)^2 ))dxdydz](https://www.tinkutara.com/question/Q83350.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{z}} \int_{{y}} ^{\mathrm{1}} .\frac{{z}^{{n}+\mathrm{1}} {Li}_{\mathrm{1}} \left({y}\right)}{{z}^{\mathrm{2}} {x}^{\mathrm{2}} }{dxdydz} \\ $$$$=\int\int\left[−{z}^{{n}−\mathrm{1}} {li}_{\mathrm{1}} \left({y}\right)+{z}^{{n}−\mathrm{1}} .\frac{{li}_{\mathrm{1}} \left({y}\right)}{{y}}\right]{dydz} \\ $$$$=\int\left({z}^{{n}−\mathrm{1}} \right)\left[\int_{\mathrm{0}\:} ^{{z}} \left\{−\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{y}^{{k}} }{{k}}+\frac{\mathrm{1}}{{y}}.\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{y}^{{k}} }{{k}}\right\}{dydz}\right. \\ $$$$=\int{z}^{{n}−\mathrm{1}} \left[\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\int_{\mathrm{0}} ^{{z}} \left\{−\frac{{y}^{{k}} }{{k}}+\frac{{y}^{{k}−\mathrm{1}} }{{k}}\right\}{dy}\right]{dz} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {z}^{{n}−\mathrm{1}} \left[\underset{{k}\geqslant\mathrm{1}} {\sum}\left\{−\frac{{z}^{{k}+\mathrm{1}} }{{k}\left({k}+\mathrm{1}\right)}+\frac{{z}^{{k}} }{{k}^{\mathrm{2}} }\right\}\right]{dz} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\left\{\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{{z}^{{n}+{k}} }{{k}\left({k}+\mathrm{1}\right)}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{z}^{{n}−\mathrm{1}+{k}} }{{k}^{\mathrm{2}} }\right\}{dz} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\left\{−\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({n}+{k}+\mathrm{1}\right)}+\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({n}+{k}\right)}\right\}= \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({k}\right)}+\frac{\mathrm{1}}{{n}\left({k}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right){n}\left({n}+{k}+\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left\{−\frac{{Li}_{\mathrm{1}} \left({x}\right)}{{n}+\mathrm{1}}+\frac{{Li}_{\mathrm{1}} \left({x}\right)−\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\left\{{Li}_{\mathrm{1}} \left({x}\right)−{H}_{{n}+\mathrm{1}} \right\}\right\} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left\{\frac{{li}_{\mathrm{1}} \left({x}\right)}{{n}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}}−\frac{{Li}_{\mathrm{1}} \left({x}\right)}{{n}\left({n}+\mathrm{1}\right)}+\frac{{H}_{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)}\right\} \\ $$$$=\frac{{H}_{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{z}} \int_{{y}} ^{\mathrm{1}} \frac{{z}^{{n}+\mathrm{1}} {Li}_{\mathrm{1}} \left({y}\right)}{\left({zx}\right)^{\mathrm{2}} }{dxdydz} \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 02/Mar/20