Question Number 150627 by puissant last updated on 14/Aug/21
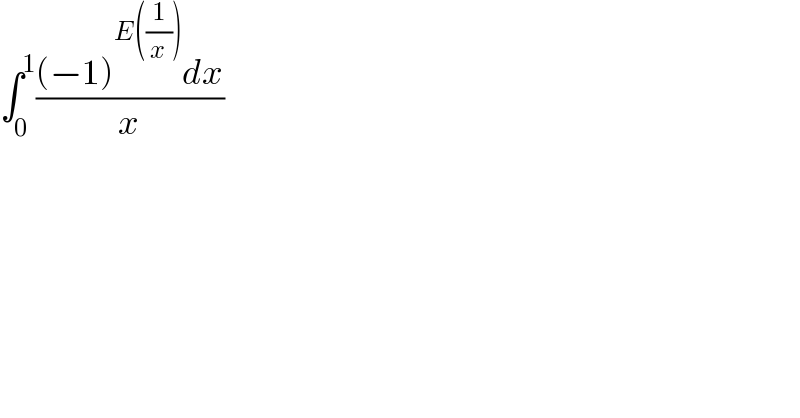
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{E}\left(\frac{\mathrm{1}}{{x}}\right)} {dx}}{{x}} \\ $$
Answered by puissant last updated on 14/Aug/21
![∫_0 ^1 (((−1)^(E((1/x))) )/x)dx ∀ x∈]0;1[, E((1/x)) existe et E((1/x))=k ⇔ k≤(1/x)<k+1 ⇔ x ∈ ](1/(k+1));(1/k)] soit X∈]0;1], ∃ ! n/ (1/(n+1))<X≤(1/n) ∧ lim_(X→0^+ ) n=+∞ on a: ∫_X ^1 (((−1)^(E((1/x))) )/x)dx =∫_X ^(1/n) (((−1)^n )/x)dx+Σ_(k=1) ^(n−1) ∫_(1/(k+1)) ^(1/k) (((−1)^k )/x)dx =(−1)^n ln((1/(nX)))+Σ_(k=1) ^(n−1) (−1)^k ln(((k+1)/k)) or (n/(n+1))<nX≤1 ⇒ lim_(X→0^+ ) ln((1/(nX)))=0 (−1)^k ln(1+(1/k)) converge. D′ou lim_(X→0^+ ) ∫_X ^1 (((−1)^(E((1/x))) )/dx)=ln((2/π))...](https://www.tinkutara.com/question/Q150674.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{E}\left(\frac{\mathrm{1}}{{x}}\right)} }{{x}}{dx} \\ $$$$\left.\forall\:{x}\in\right]\mathrm{0};\mathrm{1}\left[,\right. \\ $$$${E}\left(\frac{\mathrm{1}}{{x}}\right)\:{existe}\:{et}\:{E}\left(\frac{\mathrm{1}}{{x}}\right)={k}\:\Leftrightarrow\:{k}\leqslant\frac{\mathrm{1}}{{x}}<{k}+\mathrm{1} \\ $$$$\left.\Leftrightarrow\left.\:{x}\:\in\:\right]\frac{\mathrm{1}}{{k}+\mathrm{1}};\frac{\mathrm{1}}{{k}}\right]\: \\ $$$$\left.{s}\left.{oit}\:{X}\in\right]\mathrm{0};\mathrm{1}\right],\:\exists\:!\:{n}/\:\frac{\mathrm{1}}{{n}+\mathrm{1}}<{X}\leqslant\frac{\mathrm{1}}{{n}}\:\wedge\:{lim}_{{X}\rightarrow\mathrm{0}^{+} } {n}=+\infty \\ $$$${on}\:{a}: \\ $$$$\int_{{X}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{E}\left(\frac{\mathrm{1}}{{x}}\right)} }{{x}}{dx} \\ $$$$=\int_{{X}} ^{\frac{\mathrm{1}}{{n}}} \frac{\left(−\mathrm{1}\right)^{{n}} }{{x}}{dx}+\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{\frac{\mathrm{1}}{{k}+\mathrm{1}}} ^{\frac{\mathrm{1}}{{k}}} \frac{\left(−\mathrm{1}\right)^{{k}} }{{x}}{dx} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {ln}\left(\frac{\mathrm{1}}{{nX}}\right)+\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {ln}\left(\frac{{k}+\mathrm{1}}{{k}}\right) \\ $$$${or}\:\:\frac{{n}}{{n}+\mathrm{1}}<{nX}\leqslant\mathrm{1} \\ $$$$\Rightarrow\:{lim}_{{X}\rightarrow\mathrm{0}^{+} } {ln}\left(\frac{\mathrm{1}}{{nX}}\right)=\mathrm{0} \\ $$$$\left(−\mathrm{1}\right)^{{k}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right)\:{converge}. \\ $$$${D}'{ou}\:{lim}_{{X}\rightarrow\mathrm{0}^{+} } \int_{{X}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{E}\left(\frac{\mathrm{1}}{{x}}\right)} }{{dx}}={ln}\left(\frac{\mathrm{2}}{\pi}\right)… \\ $$
