Menu Close

0-1-1-x-2-6-dx-

Tinku Tara 0 Comments
Pin




Question Number 103312 by bemath last updated on 14/Jul/20
∫_0 ^∞ (1/((1+x^2 )^6 )) dx ?
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{6}} }\:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 14/Jul/20
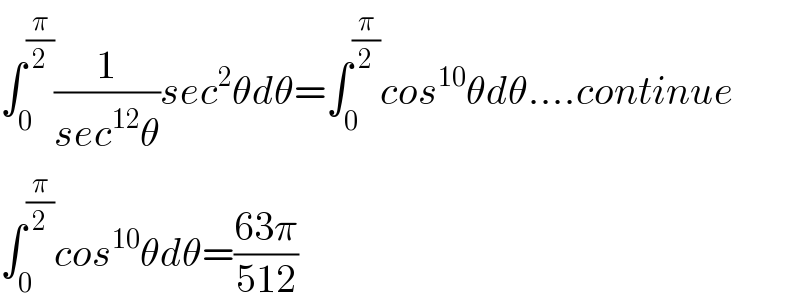
∫_0 ^(π/2) (1/(sec^(12) θ))sec^2 θdθ=∫_0 ^(π/2) cos^(10) θdθ....continue ∫_0 ^(π/2) cos^(10) θdθ=((63π)/(512))
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{sec}^{\mathrm{12}} \theta}{sec}^{\mathrm{2}} \theta{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{10}} \theta{d}\theta….{continue} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{10}} \theta{d}\theta=\frac{\mathrm{63}\pi}{\mathrm{512}} \\ $$
Commented by Ar Brandon last updated on 14/Jul/20
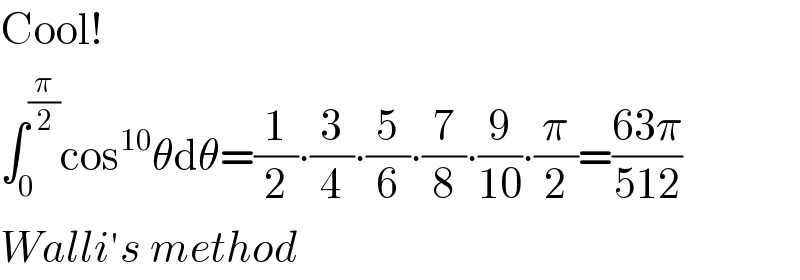
Cool! ∫_0 ^(π/2) cos^(10) θdθ=(1/2)∙(3/4)∙(5/6)∙(7/8)∙(9/(10))∙(π/2)=((63π)/(512)) Walli′s method
$$\mathrm{Cool}! \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{10}} \theta\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{7}}{\mathrm{8}}\centerdot\frac{\mathrm{9}}{\mathrm{10}}\centerdot\frac{\pi}{\mathrm{2}}=\frac{\mathrm{63}\pi}{\mathrm{512}} \\ $$$${Walli}'{s}\:{method} \\ $$
Commented by Dwaipayan Shikari last updated on 14/Jul/20
Thanking you
$${Thanking}\:{you} \\ $$
Answered by mathmax by abdo last updated on 14/Jul/20
I =∫_0 ^∞ (dx/((1+x^2 )^6 )) ⇒2I =∫_(−∞) ^(+∞) (dx/((x^2 +1)^6 )) let ϕ(z) =(1/((z^2 +1)^6 )) we have lim_(z→+∞) ∣zf(z)∣ =0 and f(z) =(1/((z−i)^6 (z+i)^6 )) so ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) Res (ϕ,i) =lim_(z→i) (1/((6−1)!)){(z−i)^6 ϕ(z)}^((5)) =lim_(z→i) (1/(5!)){(z+i)^(−6) }^((5)) =(1/(5!))(−6){(z+i)^(−7) }^((4)) =lim_(z→i) (1/(5!))(−6)(−7){(z+i)^(−8) }^((3))
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{6}} }\:\:\Rightarrow\mathrm{2I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{6}} }\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{z}\rightarrow+\infty} \mid\mathrm{zf}\left(\mathrm{z}\right)\mid\:=\mathrm{0}\:\:\mathrm{and}\:\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{6}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{6}} } \\ $$$$\mathrm{so}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\:\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{6}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{6}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{5}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{5}!}\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{6}} \right\}^{\left(\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}!}\left(−\mathrm{6}\right)\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{7}} \right\}^{\left(\mathrm{4}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{1}}{\mathrm{5}!}\left(−\mathrm{6}\right)\left(−\mathrm{7}\right)\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{8}} \right\}^{\left(\mathrm{3}\right)} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 14/Jul/20
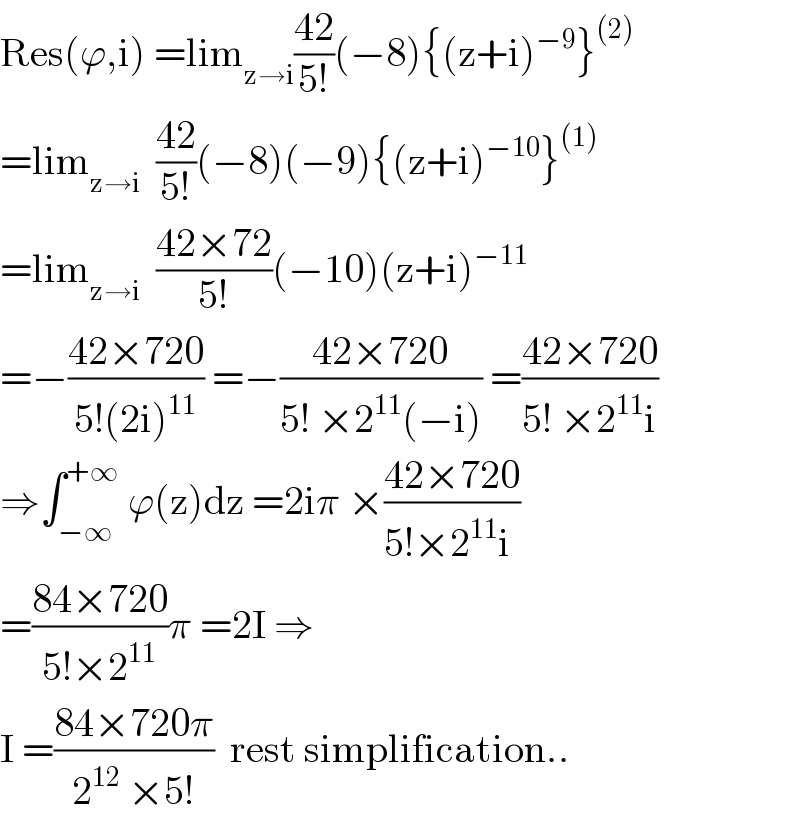
Res(ϕ,i) =lim_(z→i) ((42)/(5!))(−8){(z+i)^(−9) }^((2)) =lim_(z→i) ((42)/(5!))(−8)(−9){(z+i)^(−10) }^((1)) =lim_(z→i) ((42×72)/(5!))(−10)(z+i)^(−11) =−((42×720)/(5!(2i)^(11) )) =−((42×720)/(5! ×2^(11) (−i))) =((42×720)/(5! ×2^(11) i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ ×((42×720)/(5!×2^(11) i )) =((84×720)/(5!×2^(11) ))π =2I ⇒ I =((84×720π)/(2^(12) ×5!)) rest simplification..
$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{42}}{\mathrm{5}!}\left(−\mathrm{8}\right)\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{9}} \right\}^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{42}}{\mathrm{5}!}\left(−\mathrm{8}\right)\left(−\mathrm{9}\right)\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{10}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{42}×\mathrm{72}}{\mathrm{5}!}\left(−\mathrm{10}\right)\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{11}} \\ $$$$=−\frac{\mathrm{42}×\mathrm{720}}{\mathrm{5}!\left(\mathrm{2i}\right)^{\mathrm{11}} }\:=−\frac{\mathrm{42}×\mathrm{720}}{\mathrm{5}!\:×\mathrm{2}^{\mathrm{11}} \left(−\mathrm{i}\right)}\:=\frac{\mathrm{42}×\mathrm{720}}{\mathrm{5}!\:×\mathrm{2}^{\mathrm{11}} \mathrm{i}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:×\frac{\mathrm{42}×\mathrm{720}}{\mathrm{5}!×\mathrm{2}^{\mathrm{11}} \mathrm{i}\:} \\ $$$$=\frac{\mathrm{84}×\mathrm{720}}{\mathrm{5}!×\mathrm{2}^{\mathrm{11}} }\pi\:=\mathrm{2I}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{84}×\mathrm{720}\pi}{\mathrm{2}^{\mathrm{12}} \:×\mathrm{5}!}\:\:\mathrm{rest}\:\mathrm{simplification}.. \\ $$
Answered by OlafThorendsen last updated on 14/Jul/20
I = ∫_0 ^∞ (dx/((1+x^2 )^6 )) x = tanu dx = (1+tan^2 u)du I = ∫_0 ^(π/2) ((1+tan^2 u)/((1+tan^2 u)^6 ))du I = ∫_0 ^(π/2) (du/((1+tan^2 u)^5 )) I = ∫_0 ^(π/2) (cos^2 u)^5 du I = ∫_0 ^(π/2) cos^(10) udu I = ∫_0 ^(π/2) (((e^(iu) +e^(−iu) )/2))^(10) du I = (1/2^(10) )∫_0 ^(π/2) Σ_(k=0) ^(10) C_(10) ^k e^(iku) e^(−iu(10−k)) du I = (1/2^(10) )∫_0 ^(π/2) Σ_(k=0) ^(10) C_(10) ^k e^(2iu(k−5)) du I = (1/2^(10) )[C_(10) ^5 u+2Σ_(k=0) ^(k=4) C_(10) ^k ((sin(2u(k−5)))/(2(k−5)))]_0 ^(π/2) I = (1/2^(10) )[C_(10) ^5 (π/2)+Σ_(k=0) ^(k=4) C_(10) ^k ((sin(2π(k−5)))/((k−5)))−0] I = ((πC_(10) ^5 )/2^(11) ) I = ((63)/(512))π (≈0,387...)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{6}} } \\ $$$${x}\:=\:\mathrm{tan}{u} \\ $$$${dx}\:=\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}\right)^{\mathrm{6}} }{du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{du}}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}\right)^{\mathrm{5}} } \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} {u}\right)^{\mathrm{5}} {du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}^{\mathrm{10}} {udu} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\frac{{e}^{{iu}} +{e}^{−{iu}} }{\mathrm{2}}\right)^{\mathrm{10}} {du} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\mathrm{C}_{\mathrm{10}} ^{{k}} {e}^{{iku}} {e}^{−{iu}\left(\mathrm{10}−{k}\right)} {du} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\mathrm{C}_{\mathrm{10}} ^{{k}} {e}^{\mathrm{2}{iu}\left({k}−\mathrm{5}\right)} {du} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\left[\mathrm{C}_{\mathrm{10}} ^{\mathrm{5}} {u}+\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{k}=\mathrm{4}} {\sum}}\mathrm{C}_{\mathrm{10}} ^{{k}} \frac{\mathrm{sin}\left(\mathrm{2}{u}\left({k}−\mathrm{5}\right)\right)}{\mathrm{2}\left({k}−\mathrm{5}\right)}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\left[\mathrm{C}_{\mathrm{10}} ^{\mathrm{5}} \frac{\pi}{\mathrm{2}}+\underset{{k}=\mathrm{0}} {\overset{{k}=\mathrm{4}} {\sum}}\mathrm{C}_{\mathrm{10}} ^{{k}} \frac{\mathrm{sin}\left(\mathrm{2}\pi\left({k}−\mathrm{5}\right)\right)}{\left({k}−\mathrm{5}\right)}−\mathrm{0}\right] \\ $$$$\mathrm{I}\:=\:\frac{\pi\mathrm{C}_{\mathrm{10}} ^{\mathrm{5}} }{\mathrm{2}^{\mathrm{11}} }\: \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{63}}{\mathrm{512}}\pi\:\left(\approx\mathrm{0},\mathrm{387}…\right) \\ $$
Answered by bramlex last updated on 15/Jul/20
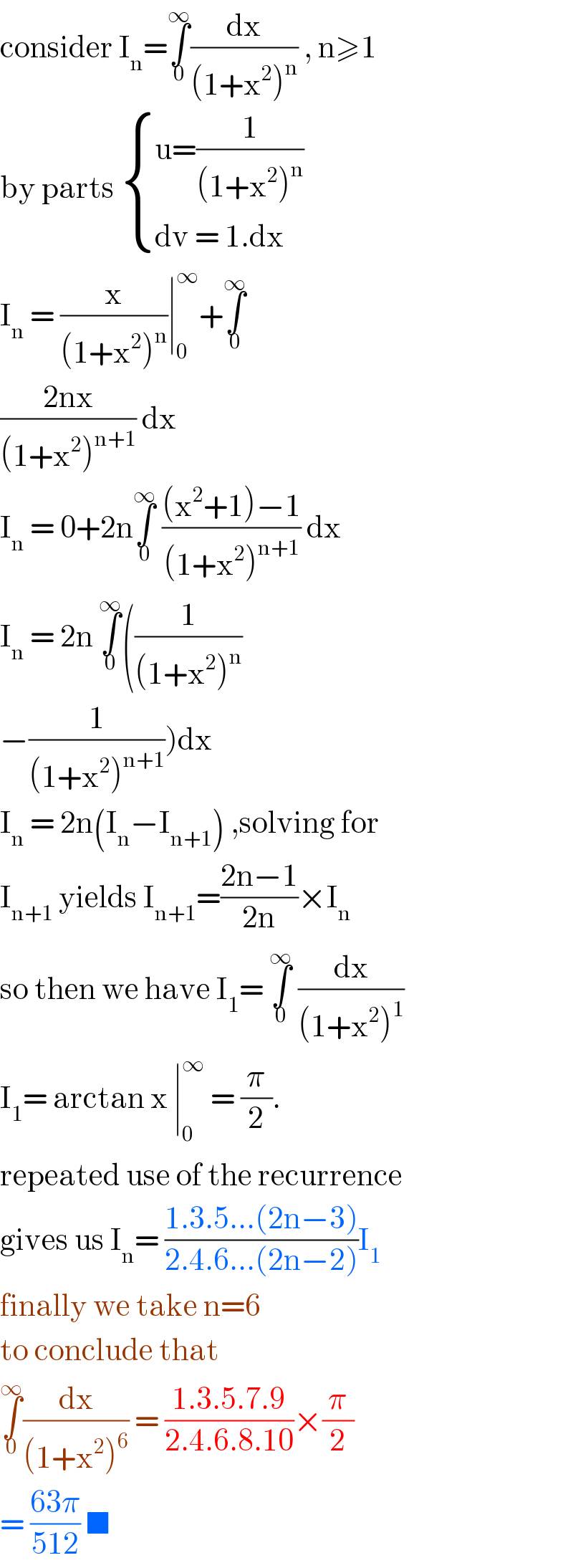
consider I_n =∫_0 ^∞ (dx/((1+x^2 )^n )) , n≥1 by parts { ((u=(1/((1+x^2 )^n )))),((dv = 1.dx)) :} I_n = (x/((1+x^2 )^n ))∣_0 ^∞ +∫_0 ^∞ ((2nx)/((1+x^2 )^(n+1) )) dx I_n = 0+2n∫_0 ^∞ (((x^2 +1)−1)/((1+x^2 )^(n+1) )) dx I_n = 2n ∫_0 ^∞ ((1/((1+x^2 )^n )) −(1/((1+x^2 )^(n+1) )))dx I_n = 2n(I_n −I_(n+1) ) ,solving for I_(n+1) yields I_(n+1) =((2n−1)/(2n))×I_n so then we have I_1 = ∫_0 ^∞ (dx/((1+x^2 )^1 )) I_1 = arctan x ∣_0 ^∞ = (π/2). repeated use of the recurrence gives us I_n = ((1.3.5...(2n−3))/(2.4.6...(2n−2)))I_1 finally we take n=6 to conclude that ∫_0 ^∞ (dx/((1+x^2 )^6 )) = ((1.3.5.7.9)/(2.4.6.8.10))×(π/2) = ((63π)/(512)) ■
$$\mathrm{consider}\:\mathrm{I}_{\mathrm{n}} =\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\:,\:\mathrm{n}\geqslant\mathrm{1} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\begin{cases}{\mathrm{u}=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }}\\{\mathrm{dv}\:=\:\mathrm{1}.\mathrm{dx}}\end{cases} \\ $$$$\mathrm{I}_{\mathrm{n}} \:=\:\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\mid_{\mathrm{0}} ^{\infty} +\underset{\mathrm{0}} {\overset{\infty} {\int}} \\ $$$$\frac{\mathrm{2nx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}+\mathrm{1}} }\:\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{n}} \:=\:\mathrm{0}+\mathrm{2n}\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}+\mathrm{1}} }\:\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{n}} \:=\:\mathrm{2n}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\right. \\ $$$$\left.−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}+\mathrm{1}} }\right)\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{n}} \:=\:\mathrm{2n}\left(\mathrm{I}_{\mathrm{n}} −\mathrm{I}_{\mathrm{n}+\mathrm{1}} \right)\:,\mathrm{solving}\:\mathrm{for} \\ $$$$\mathrm{I}_{\mathrm{n}+\mathrm{1}} \:\mathrm{yields}\:\mathrm{I}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{2n}}×\mathrm{I}_{\mathrm{n}} \\ $$$$\mathrm{so}\:\mathrm{then}\:\mathrm{we}\:\mathrm{have}\:\mathrm{I}_{\mathrm{1}} =\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{1}} } \\ $$$$\mathrm{I}_{\mathrm{1}} =\:\mathrm{arctan}\:\mathrm{x}\:\mid_{\mathrm{0}} ^{\infty} \:=\:\frac{\pi}{\mathrm{2}}. \\ $$$$\mathrm{repeated}\:\mathrm{use}\:\mathrm{of}\:\mathrm{the}\:\mathrm{recurrence} \\ $$$$\mathrm{gives}\:\mathrm{us}\:\mathrm{I}_{\mathrm{n}} =\:\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}…\left(\mathrm{2n}−\mathrm{3}\right)}{\mathrm{2}.\mathrm{4}.\mathrm{6}…\left(\mathrm{2n}−\mathrm{2}\right)}\mathrm{I}_{\mathrm{1}} \\ $$$$\mathrm{finally}\:\mathrm{we}\:\mathrm{take}\:\mathrm{n}=\mathrm{6} \\ $$$$\mathrm{to}\:\mathrm{conclude}\:\mathrm{that}\: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{6}} }\:=\:\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}.\mathrm{9}}{\mathrm{2}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\mathrm{10}}×\frac{\pi}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{63}\pi}{\mathrm{512}}\:\blacksquare\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *