Question Number 97537 by M±th+et+s last updated on 08/Jun/20
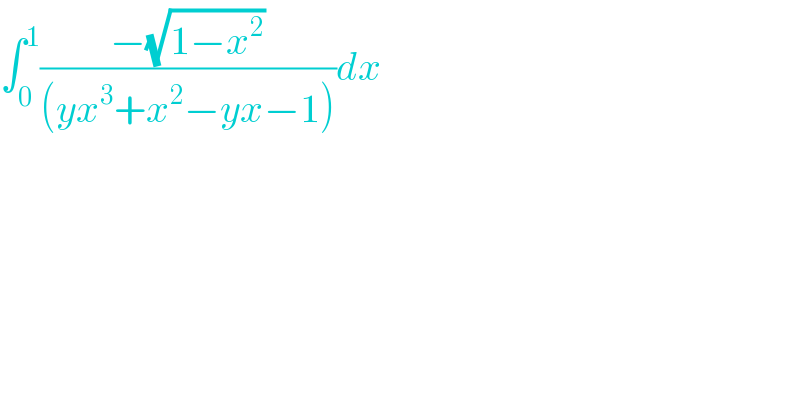
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\left({yx}^{\mathrm{3}} +{x}^{\mathrm{2}} −{yx}−\mathrm{1}\right)}{dx} \\ $$
Answered by smridha last updated on 08/Jun/20
![∫_0 ^1 (dx/((yx+1)(√(1−x^2 )))) let x=sinA =∫_0 ^(𝛑/2) (dA/(ysinA+1))=2∫_0 ^(π/2) ((d(tan(A/2)+y))/((tan(A/2)+1)^2 +((√(1−y^2 )))^2 )) =2.(1/( (√(1−y^2 ))))[tan^(−1) (((tan(A/2)+y)/( (√(1−y^2 )))))]_0 ^(𝛑/2) =(2/( (√(1−y^2 ))))[tan^(−1) (((1+y)/( (√(1−y^2 )))))−tan^(−1) ((y/( (√(1−y^2 ))))) =(1/( (√(1−y^2 ))))tan^(−1) [(((1+y)(√(1−y^2 )))/y)]](https://www.tinkutara.com/question/Q97570.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\boldsymbol{{yx}}+\mathrm{1}\right)\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\:\boldsymbol{{let}}\:\boldsymbol{{x}}=\boldsymbol{{sinA}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\boldsymbol{{dA}}}{\boldsymbol{{ysinA}}+\mathrm{1}}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\boldsymbol{{d}}\left(\boldsymbol{{tan}}\frac{\boldsymbol{{A}}}{\mathrm{2}}+\boldsymbol{{y}}\right)}{\left(\boldsymbol{{tan}}\frac{\boldsymbol{{A}}}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\boldsymbol{{tan}}\frac{\boldsymbol{{A}}}{\mathrm{2}}+{y}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\right)\right]_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\boldsymbol{{y}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\boldsymbol{{y}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\left(\mathrm{1}+\boldsymbol{{y}}\right)\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}{\boldsymbol{{y}}}\right] \\ $$
Commented by M±th+et+s last updated on 08/Jun/20

$${thank}\:{you}\:{sir} \\ $$
Commented by smridha last updated on 08/Jun/20
welcome
