Menu Close

0-1-1-x-4-x-2-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 129400 by SOMEDAVONG last updated on 15/Jan/21
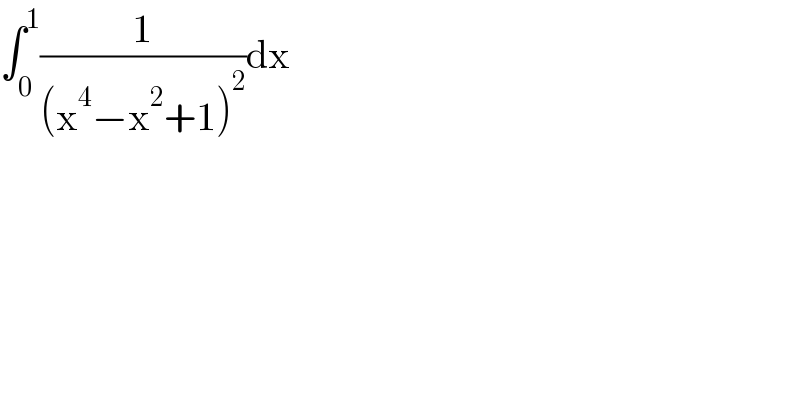
∫_0 ^1 (1/((x^4 −x^2 +1)^2 ))dx
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by MJS_new last updated on 15/Jan/21
in cases like this one I use Ostrogradski′s Method, you find it on the www ∫(dx/((x^4 −x^2 +1)^2 ))= [Ostrogradski] =((x(x^2 +1))/(6(x^4 −x^2 +1)))+(1/6)∫((x^2 +5)/(x^4 −x^2 +1))dx ∫((x^2 +5)/(x^4 −x^2 +1))dx=∫(((4(√3)x+15)/(6(x^2 +(√3)x+1)))−((4(√3)x−15)/(6(x^2 −o(√3)x+1))))dx and these should be easy to solve
$$\mathrm{in}\:\mathrm{cases}\:\mathrm{like}\:\mathrm{this}\:\mathrm{one}\:\mathrm{I}\:\mathrm{use}\:{Ostrogradski}'{s} \\ $$$${Method},\:\mathrm{you}\:\mathrm{find}\:\mathrm{it}\:\mathrm{on}\:\mathrm{the}\:\mathrm{www} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{6}\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{x}^{\mathrm{2}} +\mathrm{5}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$ \\ $$$$\int\frac{{x}^{\mathrm{2}} +\mathrm{5}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\int\left(\frac{\mathrm{4}\sqrt{\mathrm{3}}{x}+\mathrm{15}}{\mathrm{6}\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}−\frac{\mathrm{4}\sqrt{\mathrm{3}}{x}−\mathrm{15}}{\mathrm{6}\left({x}^{\mathrm{2}} −{o}\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}\right){dx} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by Ar Brandon last updated on 15/Jan/21
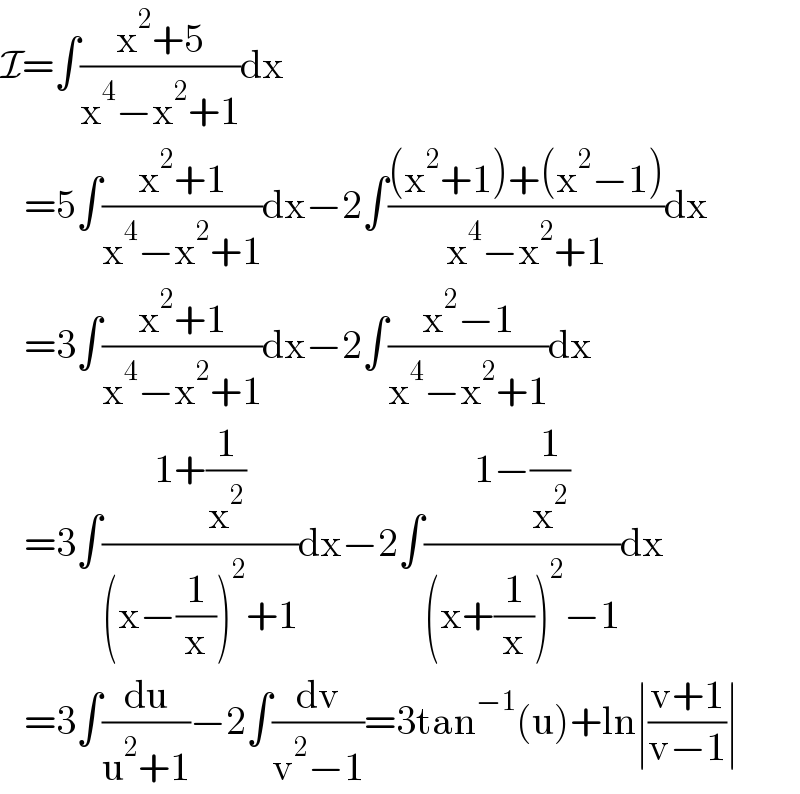
I=∫((x^2 +5)/(x^4 −x^2 +1))dx =5∫((x^2 +1)/(x^4 −x^2 +1))dx−2∫(((x^2 +1)+(x^2 −1))/(x^4 −x^2 +1))dx =3∫((x^2 +1)/(x^4 −x^2 +1))dx−2∫((x^2 −1)/(x^4 −x^2 +1))dx =3∫((1+(1/x^2 ))/((x−(1/x))^2 +1))dx−2∫((1−(1/x^2 ))/((x+(1/x))^2 −1))dx =3∫(du/(u^2 +1))−2∫(dv/(v^2 −1))=3tan^(−1) (u)+ln∣((v+1)/(v−1))∣
$$\mathcal{I}=\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{5}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{5}\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}−\mathrm{2}\int\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{3}\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}−\mathrm{2}\int\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{3}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}−\mathrm{2}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:=\mathrm{3}\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}−\mathrm{2}\int\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}}=\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{u}\right)+\mathrm{ln}\mid\frac{\mathrm{v}+\mathrm{1}}{\mathrm{v}−\mathrm{1}}\mid \\ $$
Commented by MJS_new last updated on 15/Jan/21
I get ∫(dx/((x^4 −x^2 +1)^2 ))= =((x(x^2 +1))/(6(x^4 −x^2 +1)))+((√3)/(18))ln ((x^2 +(√3)x+1)/(x^2 −(√3)x+1)) +(1/2)(arctan (2x−(√3)) +arctan (2x+(√3)))+C ⇒ ∫_0 ^1 (dx/((x^4 −x^2 +1)^2 ))=(1/3)+((√3)/9)ln (2+(√3)) +(π/4)
$$\mathrm{I}\:\mathrm{get} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{6}\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\:+\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\right)+{C} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\:+\frac{\pi}{\mathrm{4}} \\ $$
Answered by Ar Brandon last updated on 15/Jan/21
f(a)=∫_0 ^1 (dx/(x^4 −x^2 +a^2 ))=(1/(2a))∫_0 ^1 (((x^2 +a)−(x^2 −a))/(x^4 −x^2 +a^2 ))dx =(1/(2a))∫_0 ^1 {((1+(a/x^2 ))/((x−(a/x))^2 +2a^2 −1))−((1−(a/x^2 ))/((x+(a/x))^2 −2a^2 −1))}dx =(1/(2a)){∫_(−∞) ^(1−a) (du/(u^2 +((√(2a^2 −1)))^2 ))−∫_(+∞) ^(1+a) (dv/(v^2 −((√(2a^2 +1)))^2 ))} =(1/(2a)){(1/( (√(2a^2 −1))))tan^(−1) ((u/( (√(2a^2 −1)))))}_(−∞) ^(1−a) +(1/(2a)){(1/( (√(2a^2 +1))))th^(−1) ((v/( (√(2a^2 +1)))))}_(+∞) ^(1+a) ∫_0 ^1 (1/((x^4 −x^2 +1)^2 ))dx=(1/2)f ′(1)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}\right)−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}\right)}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}+\frac{\mathrm{a}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\frac{\mathrm{a}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2a}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}−\frac{\mathrm{a}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{a}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} −\mathrm{1}}\right\}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\left\{\int_{−\infty} ^{\mathrm{1}−\mathrm{a}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\left(\sqrt{\mathrm{2a}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} }−\int_{+\infty} ^{\mathrm{1}+\mathrm{a}} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\left(\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\right\} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2a}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} −\mathrm{1}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} −\mathrm{1}}}\right)\right\}_{−\infty} ^{\mathrm{1}−\mathrm{a}} +\frac{\mathrm{1}}{\mathrm{2a}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}\mathrm{th}^{−\mathrm{1}} \left(\frac{\mathrm{v}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}\right)\right\}_{+\infty} ^{\mathrm{1}+\mathrm{a}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}\:'\left(\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *