Menu Close

0-1-1-x-ln-1-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 90308 by Tony Lin last updated on 22/Apr/20
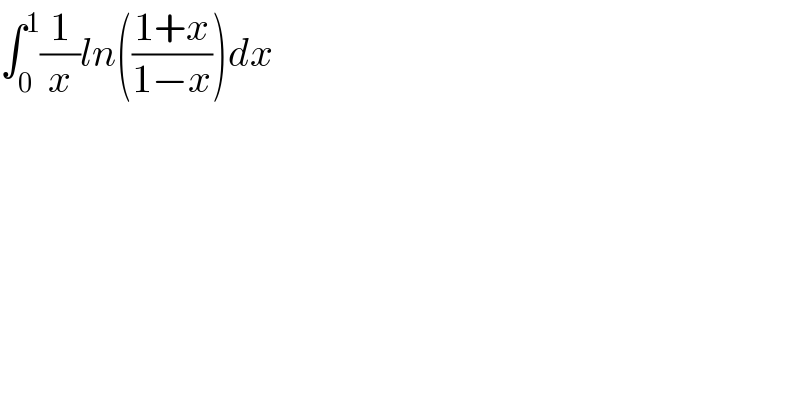
∫_0 ^1 (1/x)ln(((1+x)/(1−x)))dx
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 23/Apr/20
I =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 ((ln(1−x))/x)dx we hsve ln^′ (1+x)=(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x) =Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) +c(c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ( ∣x∣<1) ⇒((ln(1+x))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) x^(n−1) )/n) also ((ln(1−x))/x) =−Σ_(n=1) ^∞ (((−1)^(n−1) (−x)^(n−1) )/n) =−Σ_(n=1) ^∞ (x^(n−1) /n) ⇒ I =∫_0 ^1 { Σ_(n=1) ^∞ (((−1)^(n−1) x^(n−1) )/n) +Σ_(n=1) ^∞ (x^(n−1) /n)}dx =∫_0 ^1 Σ_(n=1) ^∞ (1/n)( (−1)^(n−1) +1)x^n )dx =∫_0 ^1 Σ_(n=0) ^∞ (1/(2n+1))(2) x^(2n+1) dx =2 Σ_(n=0) ^∞ (1/((2n+1))) ∫_0 ^1 x^(2n+1) dx =2 Σ_(n=0) ^∞ (1/((2n+1)(2n+2))) =Σ_(n=0) ^∞ (1/((n+1)(2n+1))) S_n =Σ_(k=0) ^n (1/((k+1)(2k+1))) ⇒(S_n /2) =Σ_(k=0) ^n (1/((2k+1)(2k+2))) =Σ_(k=0) ^n {(1/(2k+1))−(1/(2k+2))} =Σ_(k=0) ^n (1/(2k+1)) −(1/2)Σ_(k=0) ^n (1/(k+1)) Σ_(k=0) ^n (1/(k+1)) =Σ_(k=1) ^(n+1) (1/k) =H_(n+1) Σ_(k=0) ^n (1/(2k+1)) =1+(1/3) +(1/5)+....+(1/(2n+1)) =1+(1/2)+(1/3)+....+(1/(2n))+(1/(2n+1)) −(1/2)−(1/4)−....−(1/(2n)) =H_(2n+1) −(1/2)H_n ⇒ (1/2)S_n =H_(2n+1) −(1/2)H_n −(1/2)H_(n+1) =ln(2n+1)+γ +o((1/(2n+1)))−(1/2)(ln(n)+γ +ln(n+1) +γ +o((1/n))) =ln(((2n+1)/( (√(n^2 +n))))) +o((1/n))→ln(2) ⇒S_n →2ln(2)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}\:\:{we}\:{hsve} \\ $$$${ln}^{'} \left(\mathrm{1}+{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\left({c}=\mathrm{0}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}\:\:\:\:\left(\:\:\mid{x}\mid<\mathrm{1}\right)\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} }{{n}} \\ $$$${also}\:\:\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(−{x}\right)^{{n}−\mathrm{1}} }{{n}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}−\mathrm{1}} }{{n}} \\ $$$$\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{{n}−\mathrm{1}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}−\mathrm{1}} }{{n}}\right\}{dx} \\ $$$$\left.=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\left(\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} +\mathrm{1}\right){x}^{{n}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\mathrm{2}\right)\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:{dx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}+\mathrm{1}} \:{dx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\:\Rightarrow\frac{{S}_{{n}} }{\mathrm{2}}\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{2}\right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \left\{\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{2}}\right\}\:\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}+….+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+….+\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−….−\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$={H}_{\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} \:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}{S}_{{n}} ={H}_{\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}+\mathrm{1}} \\ $$$$={ln}\left(\mathrm{2}{n}+\mathrm{1}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left({n}\right)+\gamma\:+{ln}\left({n}+\mathrm{1}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right) \\ $$$$={ln}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\:\sqrt{{n}^{\mathrm{2}} \:+{n}}}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\rightarrow{ln}\left(\mathrm{2}\right)\:\Rightarrow{S}_{{n}} \rightarrow\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
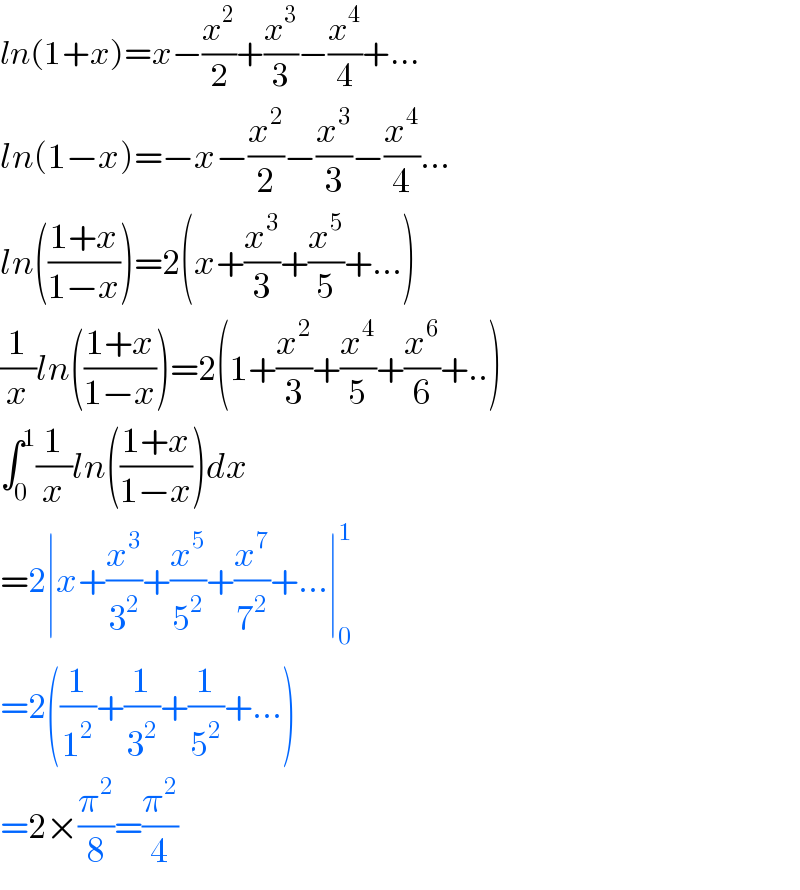
ln(1+x)=x−(x^2 /2)+(x^3 /3)−(x^4 /4)+... ln(1−x)=−x−(x^2 /2)−(x^3 /3)−(x^4 /4)... ln(((1+x)/(1−x)))=2(x+(x^3 /3)+(x^5 /5)+...) (1/x)ln(((1+x)/(1−x)))=2(1+(x^2 /3)+(x^4 /5)+(x^6 /6)+..) ∫_0 ^1 (1/x)ln(((1+x)/(1−x)))dx =2∣x+(x^3 /3^2 )+(x^5 /5^2 )+(x^7 /7^2 )+...∣_0 ^1 =2((1/1^2 )+(1/3^2 )+(1/5^2 )+...) =2×(π^2 /8)=(π^2 /4)
$${ln}\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+… \\ $$$${ln}\left(\mathrm{1}−{x}\right)=−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}… \\ $$$${ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)=\mathrm{2}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+…\right) \\ $$$$\frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)=\mathrm{2}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{5}}+\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+..\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right){dx} \\ $$$$=\mathrm{2}\mid{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{2}} }+\frac{{x}^{\mathrm{5}} }{\mathrm{5}^{\mathrm{2}} }+\frac{{x}^{\mathrm{7}} }{\mathrm{7}^{\mathrm{2}} }+…\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…\right) \\ $$$$=\mathrm{2}×\frac{\pi^{\mathrm{2}} }{\mathrm{8}}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by Tony Lin last updated on 23/Apr/20
thanks sir
$${thanks}\:{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 23/Apr/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Commented by student work last updated on 23/Apr/20
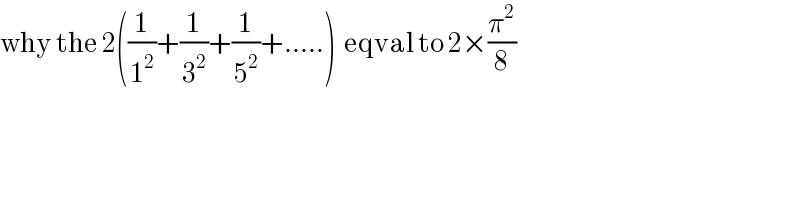
why the 2((1/1^2 )+(1/3^2 )+(1/5^2 )+.....) eqval to 2×(π^2 /8)
$$\mathrm{why}\:\mathrm{the}\:\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…..\right)\:\:\mathrm{eqval}\:\mathrm{to}\:\mathrm{2}×\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *