Menu Close

0-1-1-x-s-x-2s-

Tinku Tara 0 Comments
Pin




Question Number 126203 by frc2crc last updated on 18/Dec/20
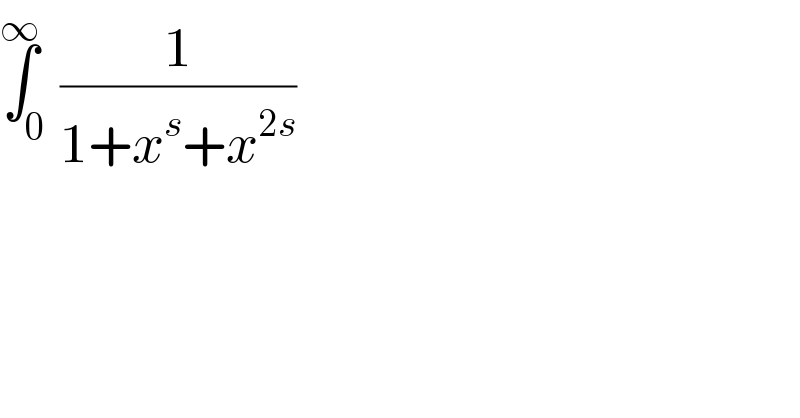
∫_0 ^∞ (1/(1+x^s +x^(2s) ))
$$\overset{\infty} {\int}_{\mathrm{0}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{s}} +{x}^{\mathrm{2}{s}} } \\ $$
Answered by Olaf last updated on 18/Dec/20
1+x^s +x^(2s) = 0 (x^s −e^(i((2π)/3)) )(x^s −e^(−i((2π)/3)) ) = 0 x = e^(i(((2π)/(3s))+((2kπ)/s))) or x = e^(i(−((2π)/(3s))+((2kπ)/s))) , k = 0...s−1 x = e^(i((2π)/s)(2k+(1/3))) or x = e^(i((2π)/s)(2k−(1/3))) , k = 0...s−1 Let x_k ^⊕ = e^(i((2π)/s)(2k+(1/3))) and x_k ^⊝ = e^(i((2π)/s)(2k−(1/3))) R(x) = (1/(1+x^s +x^(2s) )) R(x) = (1/(Π_(k=0) ^(s−1) (x−x_k ^⊕ )×Π_(k=0) ^(s−1) (x−x_k ^⊝ ))) R(x) = Σ_(p=0) ^(s−1) (A_p ^⊕ /(x−x_p ^⊕ ))+Σ_(p=0) ^(s−1) (A_p ^⊝ /(x−x_p ^⊝ )) A_p ^⊕ = (1/(Π_(k=0_(k≠p) ) ^(s−1) (x_p ^⊕ −x_k ^⊕ )×Π_(k=0) ^(s−1) (x_p ^⊕ −x_k ^⊝ ))) A_p ^⊝ = (1/(Π_(k=0) ^(s−1) (x_p ^⊝ −x_k ^⊕ )×Π_(k=0_(k≠p) ) ^(s−1) (x_p ^⊝ −x_k ^⊝ ))) I = ∫_0 ^∞ R(x)dx I = Σ_(p=0) ^(s−1) ∫_0 ^∞ [(A_p ^⊕ /(x−x_p ^⊕ ))+(A_p ^⊝ /(x−x_p ^⊝ ))]dx I = Σ_(p=0) ^(s−1) [A_p ^⊕ ln∣x−x_p ^⊕ ∣+A_p ^⊝ ln∣x−x_p ^⊝ ∣]_0 ^∞ ...to be continued... I′m not sure it′s a good way...
$$ \\ $$$$\mathrm{1}+{x}^{{s}} +{x}^{\mathrm{2}{s}} \:=\:\mathrm{0} \\ $$$$\left({x}^{{s}} −{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)\left({x}^{{s}} −{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)\:=\:\mathrm{0} \\ $$$${x}\:=\:{e}^{{i}\left(\frac{\mathrm{2}\pi}{\mathrm{3}{s}}+\frac{\mathrm{2}{k}\pi}{{s}}\right)} \:\mathrm{or}\:{x}\:=\:{e}^{{i}\left(−\frac{\mathrm{2}\pi}{\mathrm{3}{s}}+\frac{\mathrm{2}{k}\pi}{{s}}\right)} ,\:{k}\:=\:\mathrm{0}…{s}−\mathrm{1} \\ $$$${x}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{{s}}\left(\mathrm{2}{k}+\frac{\mathrm{1}}{\mathrm{3}}\right)} \:\mathrm{or}\:{x}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{{s}}\left(\mathrm{2}{k}−\frac{\mathrm{1}}{\mathrm{3}}\right)} ,\:{k}\:=\:\mathrm{0}…{s}−\mathrm{1} \\ $$$$\mathrm{Let}\:{x}_{{k}} ^{\oplus} \:=\:{e}^{{i}\frac{\mathrm{2}\pi}{{s}}\left(\mathrm{2}{k}+\frac{\mathrm{1}}{\mathrm{3}}\right)} \:\mathrm{and}\:{x}_{{k}} ^{\circleddash} \:=\:{e}^{{i}\frac{\mathrm{2}\pi}{{s}}\left(\mathrm{2}{k}−\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{s}} +{x}^{\mathrm{2}{s}} } \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{1}}{\underset{{k}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}−{x}_{{k}} ^{\oplus} \right)×\underset{{k}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}−{x}_{{k}} ^{\circleddash} \right)} \\ $$$$\mathrm{R}\left({x}\right)\:=\:\underset{{p}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\sum}}\frac{\mathrm{A}_{{p}} ^{\oplus} }{{x}−{x}_{{p}} ^{\oplus} }+\underset{{p}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\sum}}\frac{\mathrm{A}_{{p}} ^{\circleddash} }{{x}−{x}_{{p}} ^{\circleddash} } \\ $$$$\mathrm{A}_{{p}} ^{\oplus} \:=\:\frac{\mathrm{1}}{\underset{\underset{{k}\neq{p}} {{k}=\mathrm{0}}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}_{{p}} ^{\oplus} −{x}_{{k}} ^{\oplus} \right)×\underset{{k}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}_{{p}} ^{\oplus} −{x}_{{k}} ^{\circleddash} \right)} \\ $$$$\mathrm{A}_{{p}} ^{\circleddash} \:=\:\frac{\mathrm{1}}{\underset{{k}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}_{{p}} ^{\circleddash} −{x}_{{k}} ^{\oplus} \right)×\underset{\underset{{k}\neq{p}} {{k}=\mathrm{0}}} {\overset{{s}−\mathrm{1}} {\prod}}\left({x}_{{p}} ^{\circleddash} −{x}_{{k}} ^{\circleddash} \right)} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \mathrm{R}\left({x}\right){dx} \\ $$$$\mathrm{I}\:=\:\underset{{p}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\sum}}\int_{\mathrm{0}} ^{\infty} \left[\frac{\mathrm{A}_{{p}} ^{\oplus} }{{x}−{x}_{{p}} ^{\oplus} }+\frac{\mathrm{A}_{{p}} ^{\circleddash} }{{x}−{x}_{{p}} ^{\circleddash} }\right]{dx} \\ $$$$\mathrm{I}\:=\:\underset{{p}=\mathrm{0}} {\overset{{s}−\mathrm{1}} {\sum}}\left[\mathrm{A}_{{p}} ^{\oplus} \mathrm{ln}\mid{x}−{x}_{{p}} ^{\oplus} \mid+\mathrm{A}_{{p}} ^{\circleddash} \mathrm{ln}\mid{x}−{x}_{{p}} ^{\circleddash} \mid\right]_{\mathrm{0}} ^{\infty} \\ $$$$…\mathrm{to}\:\mathrm{be}\:\mathrm{continued}… \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{good}\:\mathrm{way}… \\ $$
Answered by Dwaipayan Shikari last updated on 18/Dec/20
∫_0 ^∞ (1/(1+x^s +x^(2s) ))dx x^s =t =(1/s)∫_0 ^∞ t^((1−s)/s) (1/(1+t+t^2 ))dt =(1/s)∫_0 ^∞ t^((1−s)/s) .(1/((t−e^((2iπ)/3) )(t−e^(−((2πi)/3)) )))dt =(1/(s(e^((2iπ)/3) −e^(−((2iπ)/3)) )))∫_0 ^∞ (t^a /(t−e^((2iπ)/3) ))−(1/(s(e^((2iπ)/3) −e^((−2iπ)/3) )))∫_0 ^∞ (t^a /(t−e^(−((2iπ)/3)) )) =(1/Λ)∫_0 ^∞ (t^a /(t+m))−(t^a /(t+b))dt t=my⇒1=m(dy/dt) t=bj⇒1=b(dj/dt) =(m^a /Λ)∫_0 ^∞ (y^a /(y+1))−(b^a /Λ)∫(j^a /(j+1))dj ∫_0 ^∞ (y^a /(y+1))dy (y/(y+1))=g⇒(1/((1+y)^2 ))=(dg/dy) =∫_0 ^1 y^(a−1) (g/((1−g)^2 ))dg =∫_0 ^1 g^a (1−g)^(−a−1) dg=−πcosec(πa) Similarly ∫_0 ^∞ (j^a /(j+1))=−πcosec(πa) I=−((πcosec πa)/Λ)(m^a −b^a ) (a=((1−s)/s) , Λ=2issin((2π)/3),m=−e^((2πi)/3) b=−e^((−2πi)/3) ) Not sure if it is true or not...
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{s}} +{x}^{\mathrm{2}{s}} }{dx}\:\:\:\:\:\:\:\:\:{x}^{{s}} ={t}\: \\ $$$$=\frac{\mathrm{1}}{{s}}\int_{\mathrm{0}} ^{\infty} {t}^{\frac{\mathrm{1}−{s}}{{s}}} \frac{\mathrm{1}}{\mathrm{1}+{t}+{t}^{\mathrm{2}} }{dt}\:=\frac{\mathrm{1}}{{s}}\int_{\mathrm{0}} ^{\infty} {t}^{\frac{\mathrm{1}−{s}}{{s}}} .\frac{\mathrm{1}}{\left({t}−{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \right)\left({t}−{e}^{−\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} \right)}{dt} \\ $$$$=\frac{\mathrm{1}}{{s}\left({e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \right)}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}} }{{t}−{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} }−\frac{\mathrm{1}}{{s}\left({e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{\frac{−\mathrm{2}{i}\pi}{\mathrm{3}}} \right)}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}} }{{t}−{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{1}}{\Lambda}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}} }{{t}+{m}}−\frac{{t}^{{a}} }{{t}+{b}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}={my}\Rightarrow\mathrm{1}={m}\frac{{dy}}{{dt}}\:\:\:\:{t}={bj}\Rightarrow\mathrm{1}={b}\frac{{dj}}{{dt}} \\ $$$$=\frac{{m}^{{a}} }{\Lambda}\int_{\mathrm{0}} ^{\infty} \frac{{y}^{{a}} }{{y}+\mathrm{1}}−\frac{{b}^{{a}} }{\Lambda}\int\frac{{j}^{{a}} }{{j}+\mathrm{1}}{dj} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{y}^{{a}} }{{y}+\mathrm{1}}{dy}\:\:\:\:\:\:\:\:\:\:\:\:\frac{{y}}{{y}+\mathrm{1}}={g}\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} }=\frac{{dg}}{{dy}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{a}−\mathrm{1}} \frac{{g}}{\left(\mathrm{1}−{g}\right)^{\mathrm{2}} }{dg}\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} {g}^{{a}} \left(\mathrm{1}−{g}\right)^{−{a}−\mathrm{1}} {dg}=−\pi{cosec}\left(\pi{a}\right) \\ $$$${Similarly}\:\int_{\mathrm{0}} ^{\infty} \frac{{j}^{{a}} }{{j}+\mathrm{1}}=−\pi{cosec}\left(\pi{a}\right) \\ $$$${I}=−\frac{\pi{cosec}\:\pi{a}}{\Lambda}\left({m}^{{a}} −{b}^{{a}} \right)\:\left({a}=\frac{\mathrm{1}−{s}}{{s}}\:,\:\Lambda=\mathrm{2}{issin}\frac{\mathrm{2}\pi}{\mathrm{3}},{m}=−{e}^{\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} {b}=−{e}^{\frac{−\mathrm{2}\pi{i}}{\mathrm{3}}} \right) \\ $$$${Not}\:{sure}\:{if}\:{it}\:{is}\:{true}\:{or}\:{not}… \\ $$
Answered by mathmax by abdo last updated on 19/Dec/20
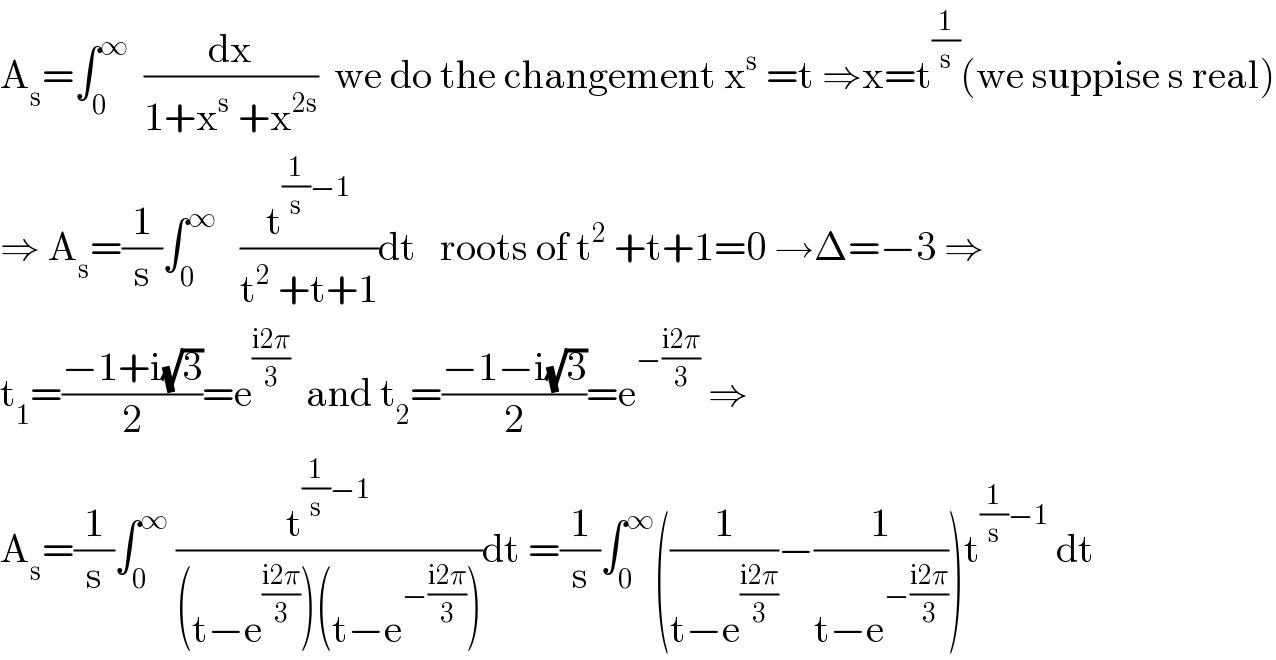
A_s =∫_0 ^∞ (dx/(1+x^s +x^(2s) )) we do the changement x^s =t ⇒x=t^(1/s) (we suppise s real) ⇒ A_s =(1/s)∫_0 ^∞ (t^((1/s)−1) /(t^2 +t+1))dt roots of t^2 +t+1=0 →Δ=−3 ⇒ t_1 =((−1+i(√3))/2)=e^((i2π)/3) and t_2 =((−1−i(√3))/2)=e^(−((i2π)/3)) ⇒ A_s =(1/s)∫_0 ^∞ (t^((1/s)−1) /((t−e^((i2π)/3) )(t−e^(−((i2π)/3)) )))dt =(1/s)∫_0 ^∞ ((1/(t−e^((i2π)/3) ))−(1/(t−e^(−((i2π)/3)) )))t^((1/s)−1) dt
$$\mathrm{A}_{\mathrm{s}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{s}} \:+\mathrm{x}^{\mathrm{2s}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{s}} \:=\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}} \left(\mathrm{we}\:\mathrm{suppise}\:\mathrm{s}\:\mathrm{real}\right) \\ $$$$\Rightarrow\:\mathrm{A}_{\mathrm{s}} =\frac{\mathrm{1}}{\mathrm{s}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{1}}\mathrm{dt}\:\:\:\mathrm{roots}\:\mathrm{of}\:\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta=−\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{s}} =\frac{\mathrm{1}}{\mathrm{s}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\left(\mathrm{t}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)\left(\mathrm{t}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{s}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} }\right)\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} \:\mathrm{dt} \\ $$
Commented by mathmax by abdo last updated on 19/Dec/20
A_s =(1/(s(2isin((π/3))))){∫_0 ^∞ (t^((1/s)−1) /(t−e^((i2π)/3) ))dt−∫_0 ^∞ (t^((1/s)−1) /(t−e^(−((i2π)/3)) ))dt} A_s =(1/(is(√3)))∫_0 ^∞ (t^((1/s)−1) /(t+e^(i(π+((2π)/3))) ))dt−(1/(is))∫_0 ^∞ (t^((1/s)−1) /(t+e^(i(π−((2π)/3))) ))dt we have ∫_0 ^∞ (t^((1/s)−1) /(t+e^(i(((5π)/3))) ))dt =_(t =e^(i((5π)/3)) z) ∫_0 ^∞ (((e^((i5π)/3) )^((1/s)−1) z^((1/s)−1) )/(e^((i5π)/3) (1+z)))e^((i5π)/3) dz = e^(((5iπ)/3)((1/s)−1)) ×(π/(sin((π/s)))) also ∫_0 ^∞ (t^((1/s)−1) /(t+e^((iπ)/3) ))dt =_(t=e^((iπ)/3) z) ∫_0 ^∞ (((e^((iπ)/3) )^((1/s)−1) z^((1/s)−1) )/(e^((iπ)/3) (1+z)))e^((iπ)/3) dz =e^(((iπ)/3)((1/s)−1)) ×(π/(sin((π/s)))) ⇒ A_s =(1/(is(√3)))×(π/(sin((π/s))))( e^(((5iπ)/3)((1/s)−1)) −e^(((iπ)/3)((1/s)−1)) ) rest to simplify A_s ...be continued...
$$\mathrm{A}_{\mathrm{s}} =\frac{\mathrm{1}}{\mathrm{s}\left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\left\{\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }\mathrm{dt}−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} }\mathrm{dt}\right\} \\ $$$$\mathrm{A}_{\mathrm{s}} =\frac{\mathrm{1}}{\mathrm{is}\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}+\mathrm{e}^{\mathrm{i}\left(\pi+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} }\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{is}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}+\mathrm{e}^{\mathrm{i}\left(\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}+\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{5}\pi}{\mathrm{3}}\right)} }\mathrm{dt}\:=_{\mathrm{t}\:=\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{3}}} \mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{e}^{\frac{\mathrm{i5}\pi}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} \mathrm{z}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{e}^{\frac{\mathrm{i5}\pi}{\mathrm{3}}} \left(\mathrm{1}+\mathrm{z}\right)}\mathrm{e}^{\frac{\mathrm{i5}\pi}{\mathrm{3}}} \:\mathrm{dz} \\ $$$$=\:\mathrm{e}^{\frac{\mathrm{5i}\pi}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}\right)} \:\:\:×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{s}}\right)}\:\mathrm{also} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{t}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} }\mathrm{dt}\:=_{\mathrm{t}=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} \mathrm{z}^{\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}} }{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{1}+\mathrm{z}\right)}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \mathrm{dz} \\ $$$$=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}\right)} ×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{s}}\right)}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{s}} =\frac{\mathrm{1}}{\mathrm{is}\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{s}}\right)}\left(\:\mathrm{e}^{\frac{\mathrm{5i}\pi}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}\right)} −\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{s}}−\mathrm{1}\right)} \right)\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{simplify}\:\mathrm{A}_{\mathrm{s}} \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *