Menu Close

0-1-1-x-x-2-x-3-x-4-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 186437 by aba last updated on 04/Feb/23
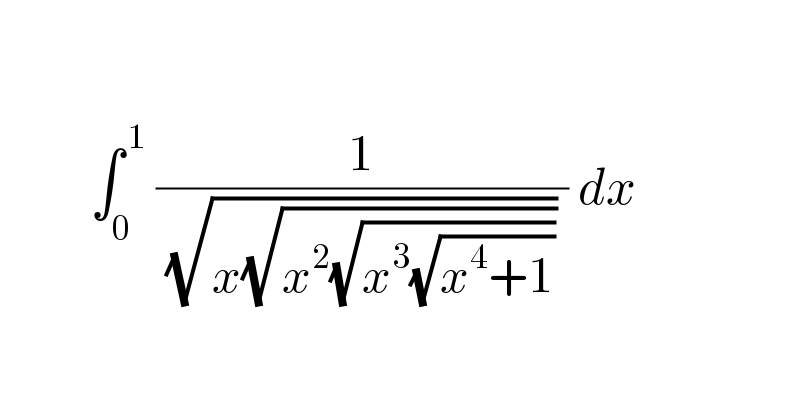
∫_0 ^( 1) (1/( (√(x(√(x^2 (√(x^3 (√(x^4 +1)))))))) )) dx
$$ \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}}\:}\:{dx} \\ $$$$\: \\ $$
Commented by Frix last updated on 04/Feb/23
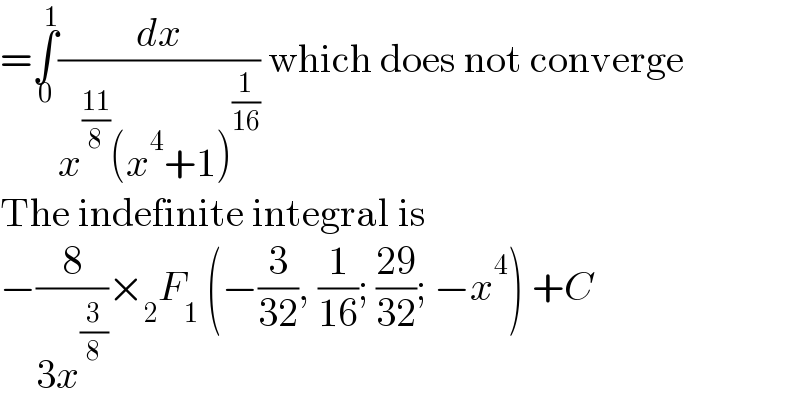
=∫_0 ^1 (dx/(x^((11)/8) (x^4 +1)^(1/(16)) )) which does not converge The indefinite integral is −(8/(3x^(3/8) ))×_2 F_1 (−(3/(32)), (1/(16)); ((29)/(32)); −x^4 ) +C
$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\frac{\mathrm{11}}{\mathrm{8}}} \left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{16}}} }\:\mathrm{which}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge} \\ $$$$\mathrm{The}\:\mathrm{indefinite}\:\mathrm{integral}\:\mathrm{is} \\ $$$$−\frac{\mathrm{8}}{\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{8}}} }×_{\mathrm{2}} {F}_{\mathrm{1}} \:\left(−\frac{\mathrm{3}}{\mathrm{32}},\:\frac{\mathrm{1}}{\mathrm{16}};\:\frac{\mathrm{29}}{\mathrm{32}};\:−{x}^{\mathrm{4}} \right)\:+{C} \\ $$
Commented by aba last updated on 04/Feb/23
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$$$ \\ $$
Answered by a.lgnaoui last updated on 04/Feb/23
(1/( (√(x^2 (√(x3(√(x^4 +1))))))))=x((1/y))^2 (1/( x^2 (√(x^3 (√(x^4 +1))))))=((x/y^2 ))^2 (1/( (√(x^3 (√(x^4 +1))))))=((x/y))^4 (1/( x^3 (√(x^4 +1))))=((x/y))^6 (1/( (√(x^4 +1))))=(x^9 /y^6 )⇒((1/y))^6 =((√(x^4 +1))/( x^9 ))(1) ((2x^3 )/( (√(x^4 +1))))=((d((√(x^4 +1)) ))/dx)(2) (1/y)=(((x^4 +1)^(−3) )/x^3 )=(1/(x^3 (x^4 +1)^3 )) (1/( (√(x(√(x^2 (√(x^3 (√(x^4 +1))))))))))=(1/(x^3 (x^4 +1)^3 )) =((2x^3 )/((x^4 +1)^3 ))×(1/(2x^6 ))=(1/(2x^6 ))((d((√(x^4 +1)) ))/dx) x^2 =t dx=(dt/(2x))=(dt/(2(√t))) (dt/( 2t(√t) (1+t^2 )^3 ))=(dt/( 2[(√t) (1+t^2 )^3 ])) =(1/(2((√t))^3 )) ×(1/((1+t^2 )^3 )) U^′ =(1/2)t^((−3)/2) V=((1/(1+t^2 )))^3 U=−t^(−(1/2)) V^′ =−2t(1+t^2 )^(−6) I=((−(√t))/((1+t^2 )^3 ))+∫((2t)/( (√t)(1+t^2 )^6 ))dt ((2t)/( (√t) (1+t^2 )))=−∫(1/( (√t)))×(d/dt)((1/(1+t^2 )))^3 I=[((−(√t))/(1+t^2 ))]−2I 3I=[((−(√t))/(1+t^2 ))]_0 ^1 ⇒I=(1/3)[((−(√t))/(1+t^2 ))]_0 ^1 ∫_0 ^1 (1/( (√(x(√(x^2 (√(x^3 (√(x^4 +1))))))))))=−(1/3)
$$\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \sqrt{{x}\mathrm{3}\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}}={x}\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}=\left(\frac{{x}}{{y}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}=\left(\frac{{x}}{{y}}\right)^{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\:{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}=\left(\frac{{x}}{{y}}\right)^{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}=\frac{{x}^{\mathrm{9}} }{{y}^{\mathrm{6}} }\Rightarrow\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{6}} =\frac{\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}{\:{x}^{\mathrm{9}} }\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{3}} }{\:\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}=\frac{{d}\left(\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:\right)}{{dx}}\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{1}}{{y}}=\frac{\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{−\mathrm{3}} }{{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{{x}^{\mathrm{3}} \left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}}}=\frac{\mathrm{1}}{{x}^{\mathrm{3}} \left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{3}} }{\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} }×\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{6}} }\frac{{d}\left(\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:\right)}{{dx}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} ={t}\:\:\:\:\:{dx}=\frac{{dt}}{\mathrm{2}{x}}=\frac{{dt}}{\mathrm{2}\sqrt{{t}}} \\ $$$$\frac{{dt}}{\:\mathrm{2}{t}\sqrt{{t}}\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{{dt}}{\:\mathrm{2}\left[\sqrt{{t}}\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} \right]}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{{t}}\right)^{\mathrm{3}} }\:×\frac{\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${U}^{'} =\frac{\mathrm{1}}{\mathrm{2}}{t}^{\frac{−\mathrm{3}}{\mathrm{2}}} \:\:\:\:{V}=\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{3}} \\ $$$${U}=−{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:{V}^{'} =−\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{−\mathrm{6}} \\ $$$${I}=\frac{−\sqrt{{t}}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }+\int\frac{\mathrm{2}{t}}{\:\sqrt{{t}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{6}} }{dt} \\ $$$$\frac{\mathrm{2}{t}}{\:\sqrt{{t}}\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=−\int\frac{\mathrm{1}}{\:\sqrt{{t}}}×\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{3}} \\ $$$${I}=\left[\frac{−\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }\right]−\mathrm{2}{I} \\ $$$$\mathrm{3}{I}=\left[\frac{−\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{−\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by aba last updated on 04/Feb/23
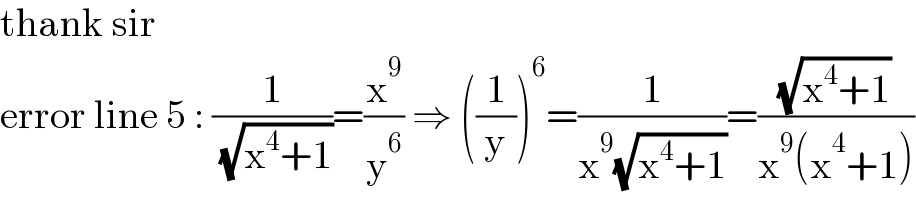
thank sir error line 5 : (1/( (√(x^4 +1))))=(x^9 /y^6 ) ⇒ ((1/y))^6 =(1/(x^9 (√(x^4 +1))))=((√(x^4 +1))/(x^9 (x^4 +1)))
$$\mathrm{thank}\:\mathrm{sir} \\ $$$$\mathrm{error}\:\mathrm{line}\:\mathrm{5}\::\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}}=\frac{\mathrm{x}^{\mathrm{9}} }{\mathrm{y}^{\mathrm{6}} }\:\Rightarrow\:\left(\frac{\mathrm{1}}{\mathrm{y}}\right)^{\mathrm{6}} =\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{9}} \sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}}=\frac{\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}}{\mathrm{x}^{\mathrm{9}} \left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)} \\ $$
Commented by aba last updated on 05/Feb/23
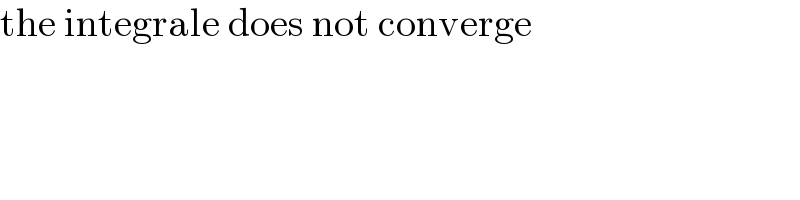
the integrale does not converge
$$\mathrm{the}\:\mathrm{integrale}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge} \\ $$
Commented by Frix last updated on 05/Feb/23
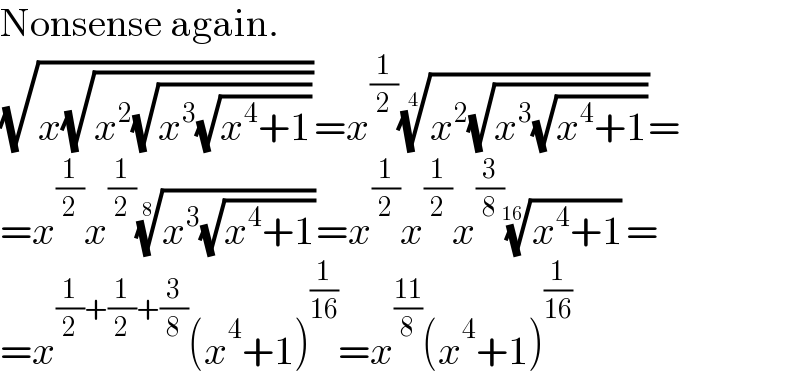
Nonsense again. (√(x(√(x^2 (√(x^3 (√(x^4 +1))))))))=x^(1/2) ((x^2 (√(x^3 (√(x^4 +1))))))^(1/4) = =x^(1/2) x^(1/2) ((x^3 (√(x^4 +1))))^(1/8) =x^(1/2) x^(1/2) x^(3/8) ((x^4 +1))^(1/(16)) = =x^((1/2)+(1/2)+(3/8)) (x^4 +1)^(1/(16)) =x^((11)/8) (x^4 +1)^(1/(16))
$$\mathrm{Nonsense}\:\mathrm{again}. \\ $$$$\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}}={x}^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt[{\mathrm{4}}]{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}}= \\ $$$$={x}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt[{\mathrm{8}}]{{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}={x}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{3}}{\mathrm{8}}} \sqrt[{\mathrm{16}}]{{x}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$={x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}} \left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{16}}} ={x}^{\frac{\mathrm{11}}{\mathrm{8}}} \left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{16}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *