Question Number 20174 by DKumar last updated on 23/Aug/17

$$\left(\mathrm{0}.\overset{−} {\mathrm{1}}\right)^{\mathrm{2}} \left\{\mathrm{1}−\mathrm{9}\left(\mathrm{0}.\mathrm{1}\overset{−} {\mathrm{6}}\right)^{\mathrm{2}} \right\} \\ $$
Answered by mrW1 last updated on 23/Aug/17
![0.1^(−) =0.111111...=(1/9) 0.16^− =0.166666...=(1/6) (0.1^− )^2 {1−9(0.16^− )^2 } =((1/9))^2 [1−3^2 ×((1/6))^2 ] =((1/9))^2 [1−((1/2))^2 ] =(1/(81))×(1+(1/2))(1−(1/2)) =(1/(81))×(3/2)×((1/2)) =(1/(27))×(1/4) =(1/(108))](https://www.tinkutara.com/question/Q20175.png)
$$\mathrm{0}.\overline {\mathrm{1}}=\mathrm{0}.\mathrm{111111}…=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{0}.\mathrm{1}\overset{−} {\mathrm{6}}=\mathrm{0}.\mathrm{166666}…=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\left(\mathrm{0}.\overset{−} {\mathrm{1}}\right)^{\mathrm{2}} \left\{\mathrm{1}−\mathrm{9}\left(\mathrm{0}.\mathrm{1}\overset{−} {\mathrm{6}}\right)^{\mathrm{2}} \right\} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{9}}\right)^{\mathrm{2}} \left[\mathrm{1}−\mathrm{3}^{\mathrm{2}} ×\left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} \right] \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{9}}\right)^{\mathrm{2}} \left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}×\frac{\mathrm{3}}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}×\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{108}} \\ $$
Answered by ajfour last updated on 23/Aug/17
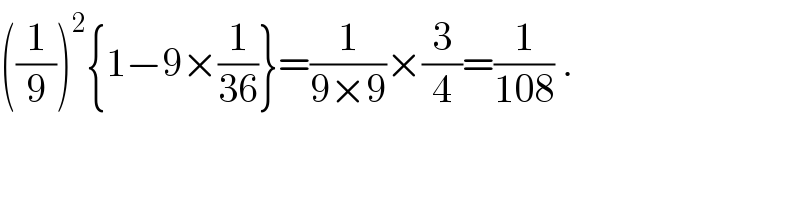
$$\left(\frac{\mathrm{1}}{\mathrm{9}}\right)^{\mathrm{2}} \left\{\mathrm{1}−\mathrm{9}×\frac{\mathrm{1}}{\mathrm{36}}\right\}=\frac{\mathrm{1}}{\mathrm{9}×\mathrm{9}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{108}}\:. \\ $$
