Menu Close

0-1-2-ix-2-dx-pi-2-

Tinku Tara 0 Comments
Pin




Question Number 120553 by snipers237 last updated on 01/Nov/20
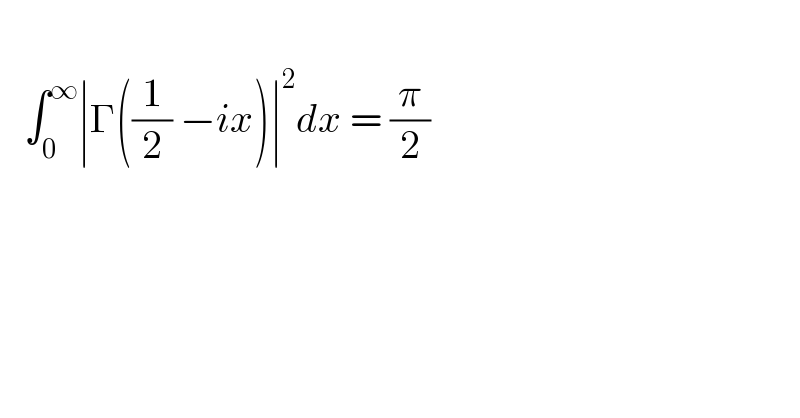
∫_0 ^∞ ∣Γ((1/2) −ix)∣^2 dx = (π/2)
$$\:\: \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\infty} \mid\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\:−{ix}\right)\mid^{\mathrm{2}} {dx}\:=\:\frac{\pi}{\mathrm{2}}\: \\ $$
Answered by mnjuly1970 last updated on 01/Nov/20
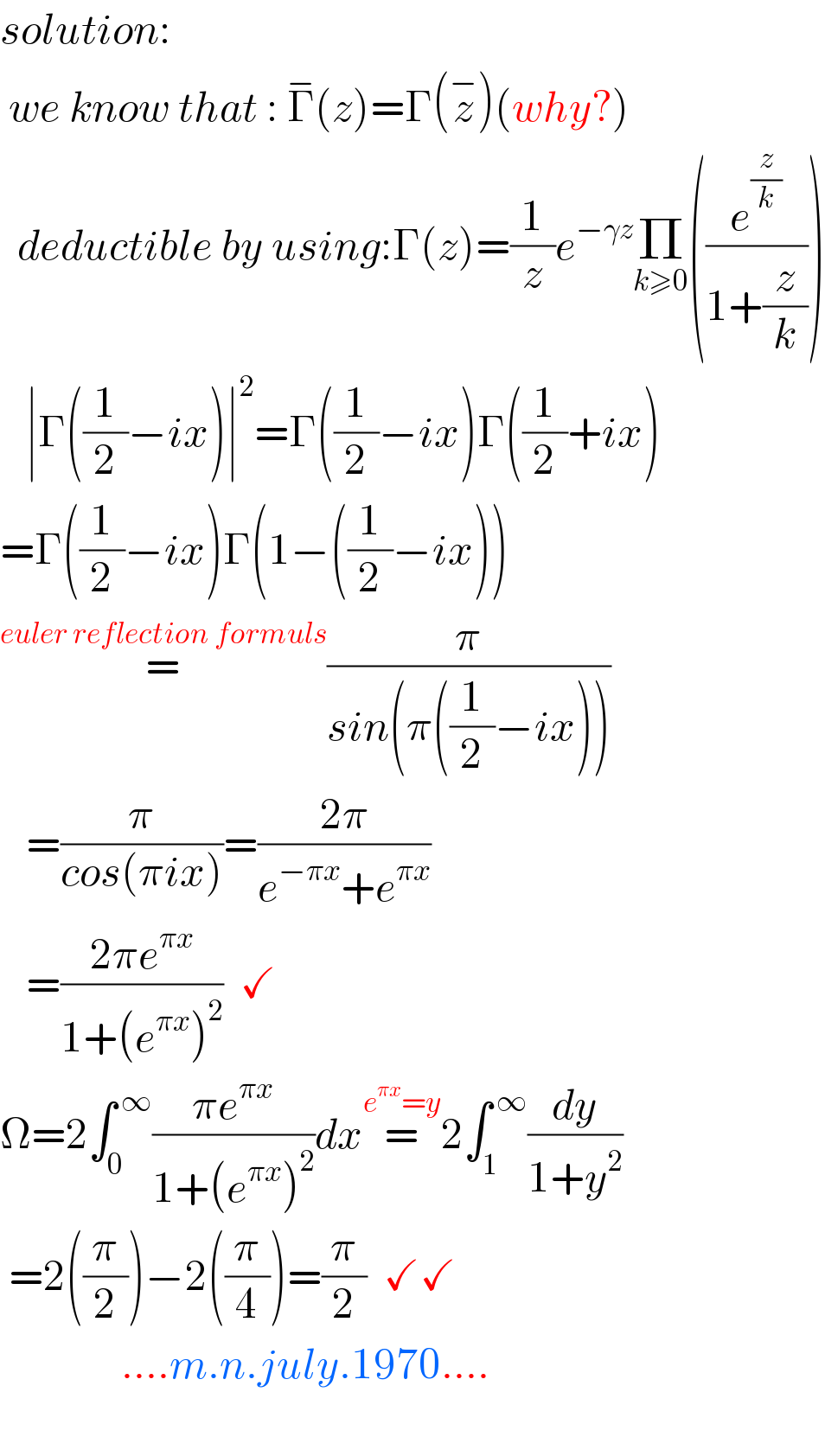
solution: we know that : Γ^− (z)=Γ(z^− )(why?) deductible by using:Γ(z)=(1/z)e^(−γz) Π_(k≥0) ((e^(z/k) /(1+(z/k)))) ∣Γ((1/2)−ix)∣^2 =Γ((1/2)−ix)Γ((1/2)+ix) =Γ((1/2)−ix)Γ(1−((1/2)−ix)) =^(euler reflection formuls) (π/(sin(π((1/2)−ix)))) =(π/(cos(πix)))=((2π)/(e^(−πx) +e^(πx) )) =((2πe^(πx) )/(1+(e^(πx) )^2 )) ✓ Ω=2∫_0 ^( ∞) ((πe^(πx) )/(1+(e^(πx) )^2 ))dx=^(e^(πx) =y) 2∫_1 ^( ∞) (dy/(1+y^2 )) =2((π/2))−2((π/4))=(π/2) ✓✓ ....m.n.july.1970....
$${solution}:\: \\ $$$$\:{we}\:{know}\:{that}\::\:\overset{−} {\Gamma}\left({z}\right)=\Gamma\left(\overset{−} {{z}}\right)\left({why}?\right) \\ $$$$\:\:{deductible}\:{by}\:{using}:\Gamma\left({z}\right)=\frac{\mathrm{1}}{{z}}{e}^{−\gamma{z}} \underset{{k}\geqslant\mathrm{0}} {\prod}\left(\frac{{e}^{\frac{{z}}{{k}}} }{\mathrm{1}+\frac{{z}}{{k}}}\right) \\ $$$$\:\:\:\mid\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\mid^{\mathrm{2}} =\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+{ix}\right) \\ $$$$=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\Gamma\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\right) \\ $$$$\overset{{euler}\:{reflection}\:{formuls}} {=}\frac{\pi}{{sin}\left(\pi\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\right)} \\ $$$$\:\:\:=\frac{\pi}{{cos}\left(\pi{ix}\right)}=\frac{\mathrm{2}\pi}{{e}^{−\pi{x}} +{e}^{\pi{x}} } \\ $$$$\:\:\:=\frac{\mathrm{2}\pi{e}^{\pi{x}} }{\mathrm{1}+\left({e}^{\pi{x}} \right)^{\mathrm{2}} }\:\:\checkmark \\ $$$$\Omega=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\pi{e}^{\pi{x}} }{\mathrm{1}+\left({e}^{\pi{x}} \right)^{\mathrm{2}} }{dx}\overset{{e}^{\pi{x}} ={y}} {=}\mathrm{2}\int_{\mathrm{1}} ^{\:\infty} \frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$\:=\mathrm{2}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\pi}{\mathrm{2}}\:\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:….{m}.{n}.{july}.\mathrm{1970}…. \\ $$$$ \\ $$
Commented by snipers237 last updated on 01/Nov/20
Γ(z) is not always equal to Γ(z^− ) but Γ^− (z)=Γ(z^− ) it′s true Γ(z)=∫_0 ^∞ t^(z−1) e^(−t) dt=∫_0 ^∞ e^((re(z)−1+iIm(z))lnt−t) dt Γ(z)=∫_0 ^∞ e^(re(z)−1−t) [cos(Im(z)lnt)+i sin(Im(z)lnt)]dt LFYTC
$$\Gamma\left({z}\right)\:{is}\:{not}\:{always}\:{equal}\:{to}\:\Gamma\left(\overset{−} {{z}}\right) \\ $$$${but}\:\:\overset{−} {\Gamma}\left({z}\right)=\Gamma\left(\overset{−} {{z}}\right)\:\:\:{it}'{s}\:{true} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{z}−\mathrm{1}} {e}^{−{t}} {dt}=\int_{\mathrm{0}} ^{\infty} {e}^{\left({re}\left({z}\right)−\mathrm{1}+{iIm}\left({z}\right)\right){lnt}−{t}} {dt} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{{re}\left({z}\right)−\mathrm{1}−{t}} \left[{cos}\left({Im}\left({z}\right){lnt}\right)+{i}\:{sin}\left({Im}\left({z}\right){lnt}\right)\right]{dt} \\ $$$${LFYTC} \\ $$
Commented by mnjuly1970 last updated on 01/Nov/20
you are right i corrected it. thank you.
$${you}\:{are}\:{right}\: \\ $$$${i}\:{corrected}\:{it}. \\ $$$${thank}\:{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *