Question Number 109136 by EmericGent last updated on 21/Aug/20

$$\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \frac{{ln}\left(\mathrm{1}-{t}\right){ln}\left({t}\right)}{{t}}\:{dt} \\ $$$${I}'{m}\:{about}\:{to}\:{give}\:{up} \\ $$
Answered by Sarah85 last updated on 21/Aug/20
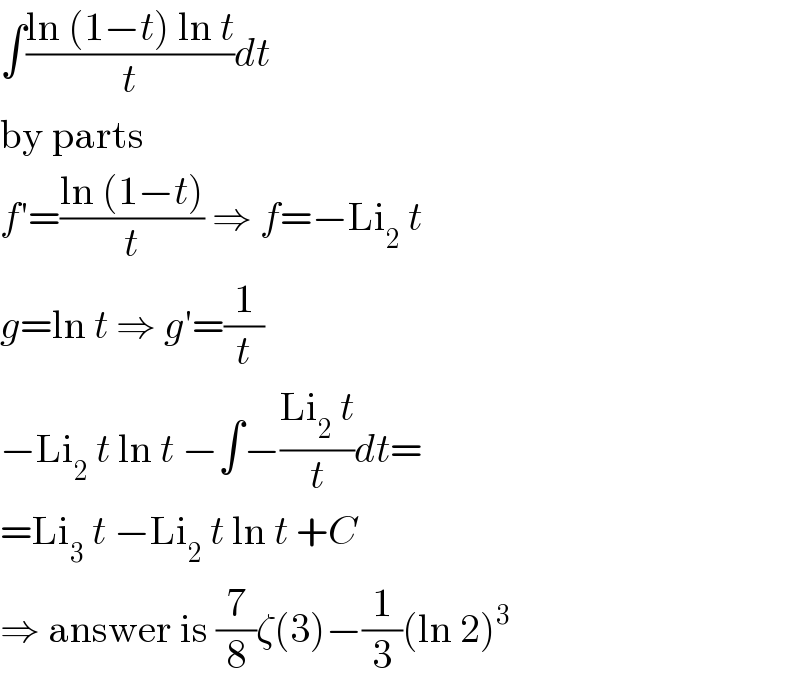
$$\int\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)\:\mathrm{ln}\:{t}}{{t}}{dt} \\ $$$$\mathrm{by}\:\mathrm{parts} \\ $$$${f}'=\frac{\mathrm{ln}\:\left(\mathrm{1}−{t}\right)}{{t}}\:\Rightarrow\:{f}=−\mathrm{Li}_{\mathrm{2}} \:{t} \\ $$$${g}=\mathrm{ln}\:{t}\:\Rightarrow\:{g}'=\frac{\mathrm{1}}{{t}} \\ $$$$−\mathrm{Li}_{\mathrm{2}} \:{t}\:\mathrm{ln}\:{t}\:−\int−\frac{\mathrm{Li}_{\mathrm{2}} \:{t}}{{t}}{dt}= \\ $$$$=\mathrm{Li}_{\mathrm{3}} \:{t}\:−\mathrm{Li}_{\mathrm{2}} \:{t}\:\mathrm{ln}\:{t}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{3}} \\ $$
