Question Number 154926 by physicstutes last updated on 23/Sep/21
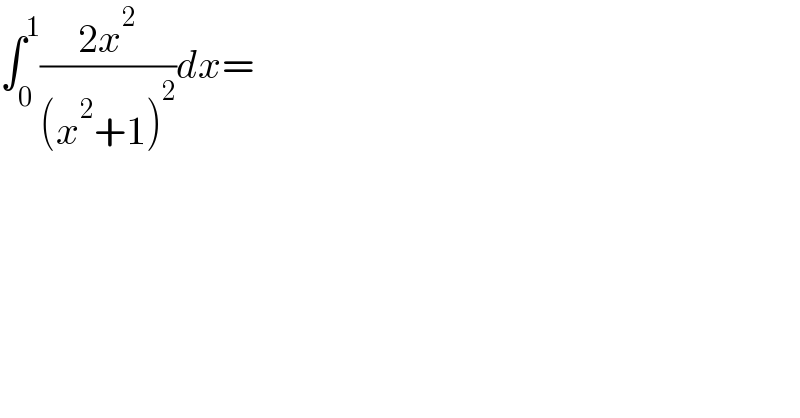
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$
Answered by qaz last updated on 23/Sep/21
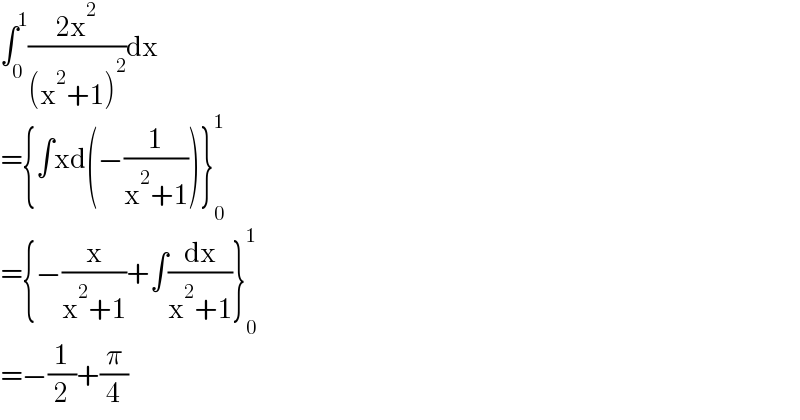
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\left\{\int\mathrm{xd}\left(−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left\{−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}} \\ $$
