Question Number 128633 by Lordose last updated on 09/Jan/21
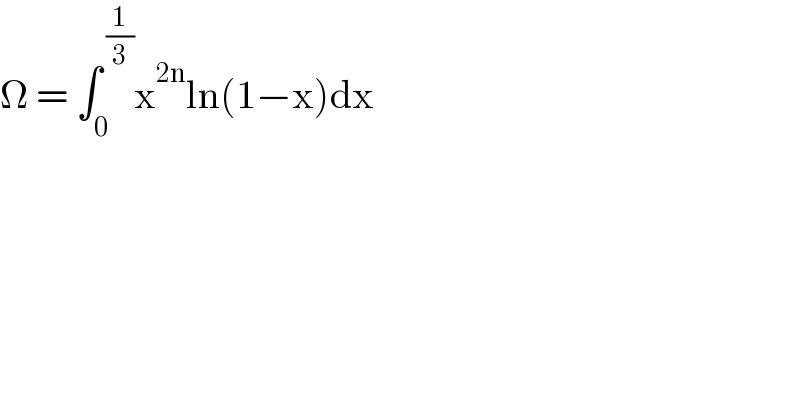
$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{x}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 09/Jan/21
![let try another way x=(t/3) ⇒ Ω=∫_0 ^1 ((t/3))^(2n) ln(1−(t/3))(dt/3) =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(((3−t)/3))dt =(1/3^(2n+1) ) ∫_0 ^1 t^(2n) ln(3−t)dt−(1/3^(2n+1) )ln(3)[(t^(2n+1) /(2n+1))]_0 ^1 =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(3−t)dt −((ln3)/((2n+1)3^(2n+1) )) we have by parts ∫_0 ^1 t^(2n) ln(3−t)dt =[(t^(2n+1) /(2n+1))ln(3−t)]_0 ^1 −∫_0 ^1 (t^(2n+1) /(2n+1))×((−1)/(3−t))dt =(1/(2n+1))ln(2)+(1/(2n+1))∫_0 ^1 (t^(2n+1) /(3−t))dt and ∫_0 ^1 (t^(2n+1) /(3−t)) dt =_(3−t=u) −∫_2 ^3 (((3−u)^(2n+1) )/u)(−du) =−∫_2 ^3 (((u−3)^(2n+1) )/u) du =−∫_2 ^3 ((Σ_(k=0) ^(2n+1) C_(2n+1) ^k u^k (−3)^(2n+1−k) )/u)du =3^(2n+1) Σ_(k=1) ^(2n+1) (−3)^(−k) C_(2n+1) ^k ∫_2 ^3 u^(k−1) du −3^(2n+1) ln((3/2)) =3^(2n+1) Σ_(k=0) ^(2n+1) (−3)^(−k) C_(2n+1) ^k (1/k){ 3^(k−1) −2^(k−1) }−3^(2n+1) ln((3/2))...](https://www.tinkutara.com/question/Q128705.png)
$$\mathrm{let}\:\mathrm{try}\:\mathrm{another}\:\mathrm{way}\:\:\mathrm{x}=\frac{\mathrm{t}}{\mathrm{3}}\:\Rightarrow \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{t}}{\mathrm{3}}\right)^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{3}}\right)\frac{\mathrm{dt}}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{2n}} \mathrm{ln}\left(\frac{\mathrm{3}−\mathrm{t}}{\mathrm{3}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{3}−\mathrm{t}\right)\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2n}+\mathrm{1}} }\mathrm{ln}\left(\mathrm{3}\right)\left[\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{3}−\mathrm{t}\right)\mathrm{dt}\:−\frac{\mathrm{ln3}}{\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{3}^{\mathrm{2n}+\mathrm{1}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{3}−\mathrm{t}\right)\mathrm{dt}\:=\left[\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{3}−\mathrm{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}×\frac{−\mathrm{1}}{\mathrm{3}−\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{3}−\mathrm{t}}\mathrm{dt}\:\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{3}−\mathrm{t}}\:\mathrm{dt}\:=_{\mathrm{3}−\mathrm{t}=\mathrm{u}} \:\:\:−\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\frac{\left(\mathrm{3}−\mathrm{u}\right)^{\mathrm{2n}+\mathrm{1}} }{\mathrm{u}}\left(−\mathrm{du}\right) \\ $$$$=−\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{\left(\mathrm{u}−\mathrm{3}\right)^{\mathrm{2n}+\mathrm{1}} }{\mathrm{u}}\:\mathrm{du}\:=−\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{u}^{\mathrm{k}} \left(−\mathrm{3}\right)^{\mathrm{2n}+\mathrm{1}−\mathrm{k}} }{\mathrm{u}}\mathrm{du} \\ $$$$=\mathrm{3}^{\mathrm{2n}+\mathrm{1}} \:\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}+\mathrm{1}} \:\left(−\mathrm{3}\right)^{−\mathrm{k}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\int_{\mathrm{2}} ^{\mathrm{3}} \:\mathrm{u}^{\mathrm{k}−\mathrm{1}} \:\mathrm{du}\:−\mathrm{3}^{\mathrm{2n}+\mathrm{1}} \mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\mathrm{3}^{\mathrm{2n}+\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\left(−\mathrm{3}\right)^{−\mathrm{k}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\frac{\mathrm{1}}{\mathrm{k}}\left\{\:\mathrm{3}^{\mathrm{k}−\mathrm{1}} −\mathrm{2}^{\mathrm{k}−\mathrm{1}} \right\}−\mathrm{3}^{\mathrm{2n}+\mathrm{1}} \mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)… \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 09/Jan/21
![Ω=∫_0 ^(1/3) x^(2n) ln(1−x)dx by parts u^′ =x^(2n) [and v=ln(1−x) Ω=[(x^(2n+1) /(2n+1))ln(1−x)]_0 ^(1/3) −∫_0 ^(1/3) (x^(2n+1) /(2n+1))×((−1)/(1−x))dx =(1/(2n+1(3)^(2n+1) ))ln((2/3))+(1/(2n+1))∫_0 ^(1/3) (x^(2n+1) /(1−x))dx but ∫_0 ^(1/3) (x^(2n+1) /(1−x))dx =∫_0 ^(1/3) ((x^(2n+1) −1+1)/(1−x))dx =∫_0 ^(1/3) (((x−1)(1+x+x^2 +...+x^(2n) ))/(1−x))dx +[−ln(1−x)]_0 ^(1/3) =−∫_0 ^(1/3) (Σ_(k=0) ^(2n) x^k )dx−ln((2/3)) =−Σ_(k=0) ^(2n) [(x^(k+1) /(k+1))]_0 ^(1/3) −ln2 +ln3 =−Σ_(k=0) ^(2n) (1/((k+1)3^(k+1) )) +ln3−ln2 rsst to find the value of this serie...](https://www.tinkutara.com/question/Q128703.png)
$$\Omega=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\mathrm{x}^{\mathrm{2n}} \left[\mathrm{and}\:\mathrm{v}=\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right. \\ $$$$\Omega=\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} −\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}×\frac{−\mathrm{1}}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}\left(\mathrm{3}\right)^{\mathrm{2n}+\mathrm{1}} }\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\mathrm{1}+\mathrm{1}}{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:+…+\mathrm{x}^{\mathrm{2n}} \right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$+\left[−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:=−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{x}^{\mathrm{k}} \right)\mathrm{dx}−\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\left[\frac{\mathrm{x}^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:−\mathrm{ln2}\:+\mathrm{ln3} \\ $$$$=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{3}^{\mathrm{k}+\mathrm{1}} }\:+\mathrm{ln3}−\mathrm{ln2}\:\:\mathrm{rsst}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}… \\ $$
