Question Number 88007 by Mikael_786 last updated on 07/Apr/20
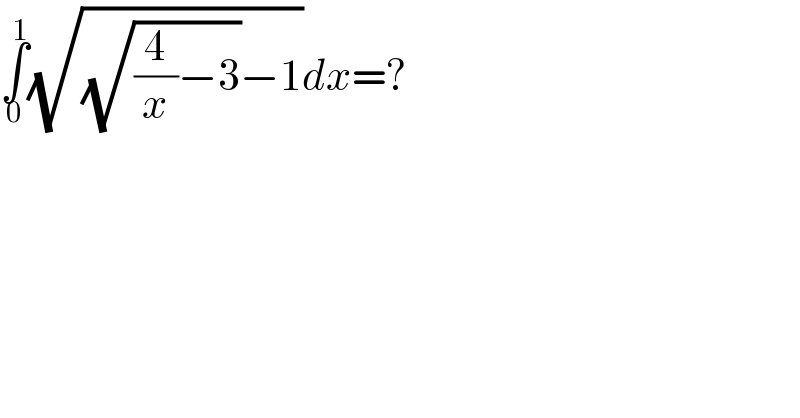
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}{dx}=? \\ $$
Answered by MJS last updated on 07/Apr/20
![t=(√((√((4/x)−3))−1)) → dx=−x^2 (√((4/x)−3))(√((√((4/x)−3))−1))dt ⇒ ∫(√((√((4/x)−3))−1))dx=−16∫((t^2 (t^2 +1))/((t^4 +2t^2 +4)^2 ))dt= [Ostrogradski again] =((4t)/(t^4 +2t^2 +4))−4∫(dt/(t^4 +2t^2 +4)) ∫(dt/(t^4 +2t^2 +4))=−((√2)/8)∫((t−(√2))/(t^2 −(√2)t+2))dt+((√2)/8)∫((t+(√2))/(t^2 +(√2)t+2))dt= =−((√2)/(16))ln (t^2 −(√2)t+2) +((√6)/(24))arctan (((√3)((√2)t−1))/3) + +((√2)/(16))ln (t^2 +(√2)t+2) +((√6)/(24))arctan (((√3)((√2)t+1))/3) = =((√2)/(16))ln ((t^2 +(√2)t+2)/(t^2 −(√2)t+2)) +((√6)/(24))(arctan (((√3)((√2)t−1))/3) +arctan (((√3)((√2)t+1))/3)) ⇒ ∫(√((√((4/x)−3))−1))dx= =((4t)/(t^4 +2t^2 +4))+((√2)/4)ln ((t^2 −(√2)t+2)/(t^2 +(√2)t+2)) −((√6)/6)(arctan (((√3)((√2)t−1))/3) +arctan (((√3)((√2)t+1))/3)) +C with t=(√((√((4/x)−3))−1)) ⇒ ∫_0 ^1 (√((√((4/x)−3))−1))dx=(π/( (√6)))](https://www.tinkutara.com/question/Q88025.png)
$${t}=\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}\:\rightarrow\:{dx}=−{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}{dt} \\ $$$$\Rightarrow \\ $$$$\int\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}{dx}=−\mathrm{16}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\:\mathrm{again}\right] \\ $$$$=\frac{\mathrm{4}{t}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}}−\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}} \\ $$$$ \\ $$$$\int\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\frac{{t}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{2}}{dt}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\frac{{t}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{2}}{dt}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{2}\right)\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+ \\ $$$$\:\:\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{2}\right)\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}{\mathrm{3}}\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{2}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{2}}\:+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}{\mathrm{3}}\right) \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\int\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{4}{t}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{2}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{2}}\:−\frac{\sqrt{\mathrm{6}}}{\mathrm{6}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}{\mathrm{3}}\right)\:+{C} \\ $$$$\mathrm{with}\:{t}=\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\sqrt{\frac{\mathrm{4}}{{x}}−\mathrm{3}}−\mathrm{1}}{dx}=\frac{\pi}{\:\sqrt{\mathrm{6}}} \\ $$
Commented by Mikael_786 last updated on 08/Apr/20

$${thankfull}\:{Bro} \\ $$
