Question Number 26950 by Joel578 last updated on 31/Dec/17

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{6}{x}^{\mathrm{2}} \:−\:{x}\:−\:\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} \:−\:\mathrm{5}{x}\:+\:\mathrm{1}}\:{dx} \\ $$
Commented by prakash jain last updated on 31/Dec/17

$$\mathrm{Integral}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$
Commented by Joel578 last updated on 01/Jan/18
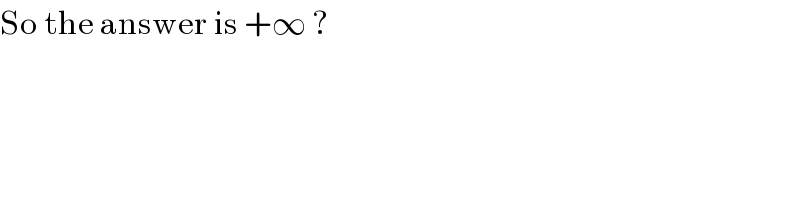
$$\mathrm{So}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:+\infty\:? \\ $$
Commented by prakash jain last updated on 01/Jan/18

$$\frac{\mathrm{6}{x}^{\mathrm{2}} −{x}−\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{1}}=\frac{\left(\mathrm{3}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)}{\left(\mathrm{3}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)} \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}{x}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}{x}−\mathrm{1}}{dx} \\ $$$$\mathrm{integral}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}\:{x}=\frac{\mathrm{1}}{\mathrm{3}}. \\ $$$$\mathrm{Also}\:\mathrm{if}\:\mathrm{you}\:\mathrm{split}\:\mathrm{integral}\:\mathrm{integral}\:\mathrm{in} \\ $$$$\mathrm{two}\:\mathrm{parts}\:\mathrm{one}\:\mathrm{part}\:\mathrm{is}\:+\infty\:\mathrm{and}\:\mathrm{other} \\ $$$$\mathrm{is}\:−\infty. \\ $$$$\mathrm{You}\:\mathrm{could}\:\mathrm{use}\:\mathrm{Cauchy}\:\mathrm{priciple} \\ $$$$\mathrm{value}\:\mathrm{to}\:\mathrm{compute}\:\mathrm{the}\:\mathrm{integral} \\ $$$$\mathrm{which}\:\mathrm{will}\:\mathrm{be}\:\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}.\: \\ $$
