Question Number 117403 by bemath last updated on 11/Oct/20
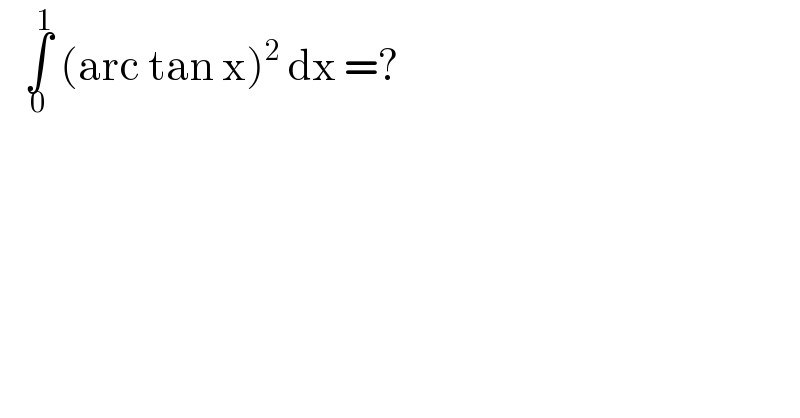
$$\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{arc}\:\mathrm{tan}\:\mathrm{x}\right)^{\mathrm{2}} \:\mathrm{dx}\:=? \\ $$
Commented by MJS_new last updated on 11/Oct/20
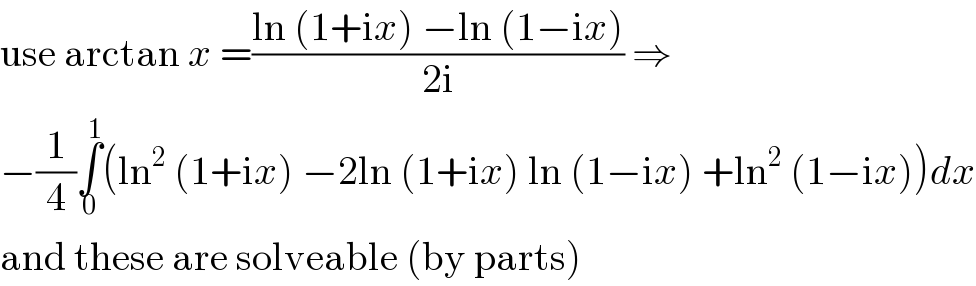
$$\mathrm{use}\:\mathrm{arctan}\:{x}\:=\frac{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{i}{x}\right)\:−\mathrm{ln}\:\left(\mathrm{1}−\mathrm{i}{x}\right)}{\mathrm{2i}}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}+\mathrm{i}{x}\right)\:−\mathrm{2ln}\:\left(\mathrm{1}+\mathrm{i}{x}\right)\:\mathrm{ln}\:\left(\mathrm{1}−\mathrm{i}{x}\right)\:+\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}−\mathrm{i}{x}\right)\right){dx} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{solveable}\:\left(\mathrm{by}\:\mathrm{parts}\right) \\ $$
Answered by mindispower last updated on 11/Oct/20
![=[xarctan^2 (x)]_0 ^1 −∫_0 ^1 ((2x)/(1+x^2 ))arctan(x)dx =(π^2 /(16))−I let arctan(x)=t I=−∫_0 ^(π/4) ((2tg(t)t)/(1+tg^2 (t))).(1+tg^2 (t))dt =−2∫_0 ^(π/4) tg(t)tdt by part=−2([−tln(cost)]_0 ^(π/4) +∫_0 ^(π/4) ln(cos(t))dt =−(π/4)ln(2)−2∫_0 ^(π/4) ln(cos(t))dt one way too find it let a=∫_0 ^(π/4) ln(cos(t))dt =∫_0 ^(π/4) (1/2)ln(sin(t)cos(t).(1/(tg(t))))dt =∫_0 ^(π/4) ((ln(((sin(2t))/2)))/2)dt−(1/2)∫_0 ^(π/4) ln(tg(t))dt_(tg(t)=s) 2t=u⇒(1/4)∫_0 ^(π/2) ln(u)du−∫_0 ^(π/4) ln(2)du in first ∫_0 ^(π/4) ln(tg(t))dt=∫_0 ^1 ((ln(s))/(1+s^2 ))ds=Σ∫_0 ^1 (−1)^k s^(2k+1) ln(s)ds =−Σ(−1)^k .(1/((2k+1)^2 ))=−β(2) =−G ,G catalan constante knowing∫_0 ^(π/2) ln(sin(t))dt give us close forme 2nd use fourier serie of ln(cos(t))=−ln(2)−Σ_(n≥1) ((cos(2(2n−1)t))/(2n−1)) give use resulte imediatly withe Σ_(n≥1) (((−1)^(n−1) )/((2n−1)^2 )) =β(2)](https://www.tinkutara.com/question/Q117462.png)
$$=\left[{xarctan}^{\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{arctan}\left({x}\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−{I} \\ $$$${let}\:{arctan}\left({x}\right)={t} \\ $$$${I}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{2}{tg}\left({t}\right){t}}{\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)}.\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right){dt} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}\left({t}\right){tdt}\:{by}\:{part}=−\mathrm{2}\left(\left[−{tln}\left({cost}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \right. \\ $$$$+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$${one}\:{way}\:{too}\:{find}\:{it} \\ $$$${let}\:{a}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\mathrm{2}}{ln}\left({sin}\left({t}\right){cos}\left({t}\right).\frac{\mathrm{1}}{{tg}\left({t}\right)}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{ln}\left(\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)}{\mathrm{2}}{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tg}\left({t}\right)\right){dt}_{{tg}\left({t}\right)={s}} \\ $$$$\mathrm{2}{t}={u}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({u}\right){du}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{2}\right){du}\:{in}\:{first} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tg}\left({t}\right)\right){dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{\mathrm{1}+{s}^{\mathrm{2}} }{ds}=\Sigma\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} {s}^{\mathrm{2}{k}+\mathrm{1}} {ln}\left({s}\right){ds} \\ $$$$=−\Sigma\left(−\mathrm{1}\right)^{{k}} .\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }=−\beta\left(\mathrm{2}\right)\:=−{G}\:,{G}\:{catalan}\:{constante} \\ $$$${knowing}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({t}\right)\right){dt}\:{give}\:{us}\:{close}\:{forme} \\ $$$$\mathrm{2}{nd}\:{use}\:{fourier}\:{serie}\:{of}\: \\ $$$${ln}\left({cos}\left({t}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right){t}\right)}{\mathrm{2}{n}−\mathrm{1}} \\ $$$${give}\:{use}\:{resulte}\:{imediatly} \\ $$$${withe}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:=\beta\left(\mathrm{2}\right) \\ $$
