Question Number 126997 by bramlexs22 last updated on 26/Dec/20
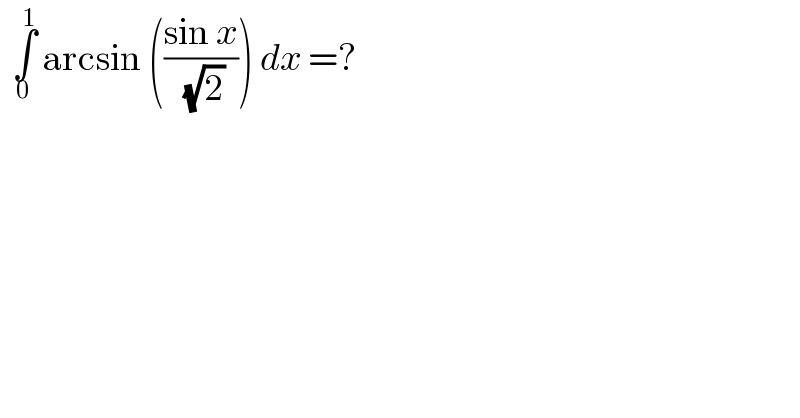
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{arcsin}\:\left(\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\:{dx}\:=? \\ $$
Answered by Evimene last updated on 26/Dec/20
![solution let (√2)=α f(α)=∫_0 ^1 arcsin(((sinx)/α))dx⇔differentiating α f′(α)=∫_0 ^1 (α^2 /(α^2 −sin^2 x))dx⇔multiply by ((sec^2 x)/(sec^2 x)) f^′ (α)=∫_0 ^1 ((α^2 sec^2 x)/(α^2 sec^2 x−α^2 tan^2 x))dx⇔recall sec^2 x+tan^2 x=1 f′(α)=∫_0 ^1 sec^2 xdx;⇔[tanx]_0 ^1 f^1 (α)=(π/4) f(α)=(π/4)x+c⇔f(0)=0;so c=0 f(α)=(π/4) cadet praise](https://www.tinkutara.com/question/Q127001.png)
$$\mathrm{solution} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{2}}=\alpha \\ $$$$\mathrm{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arcsin}\left(\frac{\mathrm{sinx}}{\alpha}\right)\mathrm{dx}\Leftrightarrow\mathrm{differentiating}\:\alpha \\ $$$$\mathrm{f}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\Leftrightarrow\mathrm{multiply}\:\mathrm{by}\:\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{f}^{'} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\alpha^{\mathrm{2}} \mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\alpha^{\mathrm{2}} \mathrm{sec}^{\mathrm{2}} \mathrm{x}−\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\Leftrightarrow\mathrm{recall}\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}=\mathrm{1} \\ $$$$\mathrm{f}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sec}^{\mathrm{2}} \mathrm{xdx};\Leftrightarrow\left[\mathrm{tanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{f}^{\mathrm{1}} \left(\alpha\right)=\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{f}\left(\alpha\right)=\frac{\pi}{\mathrm{4}}\mathrm{x}+\mathrm{c}\Leftrightarrow\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0};\mathrm{so}\:\mathrm{c}=\mathrm{0} \\ $$$$\mathrm{f}\left(\alpha\right)=\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{cadet}\:\mathrm{praise} \\ $$
Commented by bramlexs22 last updated on 26/Dec/20
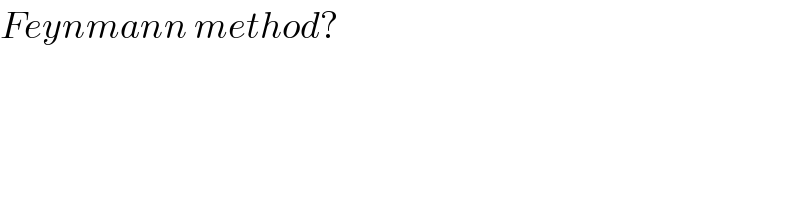
$${Feynmann}\:{method}? \\ $$
