Question Number 157750 by cortano last updated on 27/Oct/21
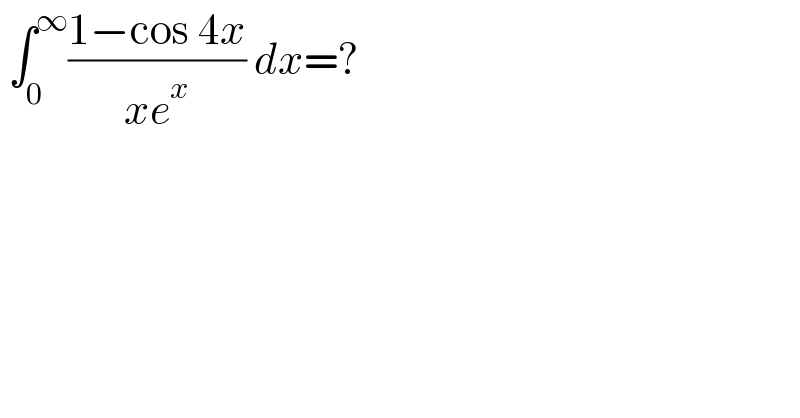
$$\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}}{{xe}^{{x}} }\:{dx}=? \\ $$
Answered by qaz last updated on 27/Oct/21
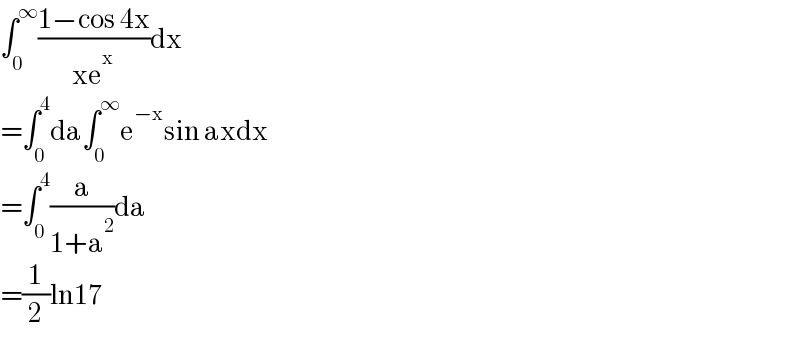
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4x}}{\mathrm{xe}^{\mathrm{x}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{da}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\mathrm{axdx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{da} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln17} \\ $$
