Question Number 92344 by 675480065 last updated on 06/May/20
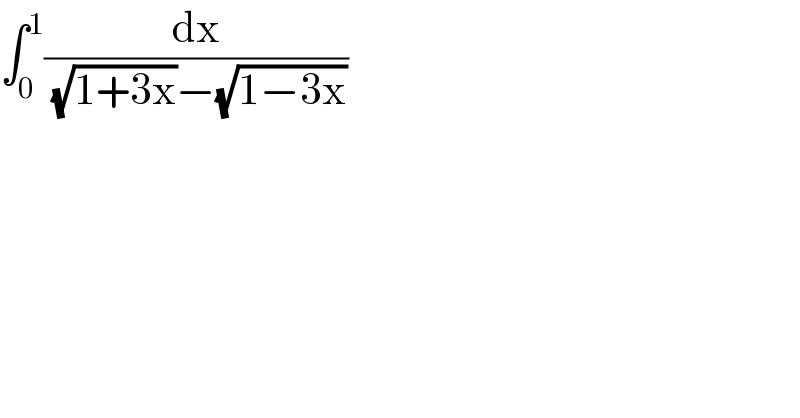
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{3x}}−\sqrt{\mathrm{1}−\mathrm{3x}}} \\ $$
Commented by john santu last updated on 06/May/20
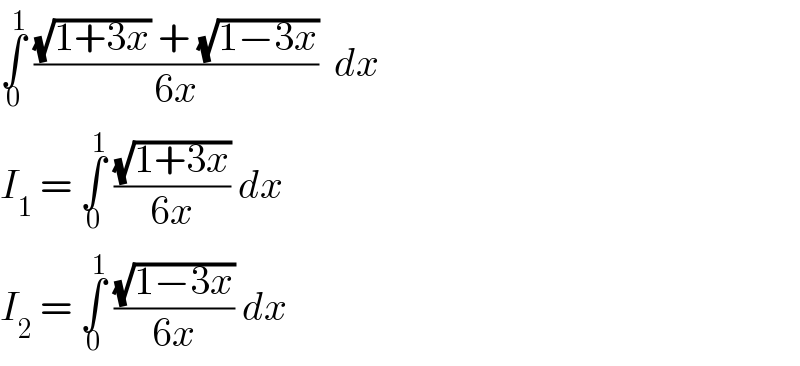
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\sqrt{\mathrm{1}+\mathrm{3}{x}}\:+\:\sqrt{\mathrm{1}−\mathrm{3}{x}}}{\mathrm{6}{x}}\:\:{dx}\: \\ $$$${I}_{\mathrm{1}} \:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\sqrt{\mathrm{1}+\mathrm{3}{x}}}{\mathrm{6}{x}}\:{dx} \\ $$$${I}_{\mathrm{2}} \:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\sqrt{\mathrm{1}−\mathrm{3}{x}}}{\mathrm{6}{x}}\:{dx}\: \\ $$
Commented by 675480065 last updated on 06/May/20

$$\mathrm{thnks}\:\mathrm{sir}\: \\ $$$$\mathrm{i}\:\mathrm{cant}\:\mathrm{continue} \\ $$
Commented by mathmax by abdo last updated on 06/May/20

$${this}\:{integral}\:{is}\:{divergent}\:\:\:\sqrt{\mathrm{1}+\mathrm{3}{x}}\sim\mathrm{1}+\frac{\mathrm{3}{x}}{\mathrm{2}}\:\:{and}\:\sqrt{\mathrm{1}−\mathrm{3}{x}}\sim\mathrm{1}−\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{1}+\mathrm{3}{x}}−\sqrt{\mathrm{1}−\mathrm{3}{x}}\sim\mathrm{3}{x}\:\Rightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{3}{x}}−\sqrt{\mathrm{1}−\mathrm{3}{x}}}\:\sim\frac{\mathrm{1}}{\mathrm{3}{x}}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{3}{x}}\:\:\:{is}\:{divergent}…! \\ $$
