Question Number 182183 by amin96 last updated on 05/Dec/22
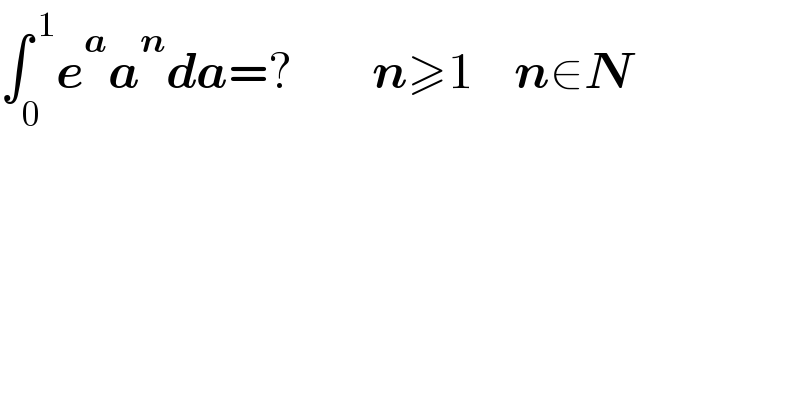
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \boldsymbol{{e}}^{\boldsymbol{{a}}} \boldsymbol{{a}}^{\boldsymbol{{n}}} \boldsymbol{{da}}=?\:\:\:\:\:\:\:\:\boldsymbol{{n}}\geqslant\mathrm{1}\:\:\:\:\boldsymbol{{n}}\in\boldsymbol{{N}} \\ $$
Answered by mr W last updated on 06/Dec/22
![I_n =∫_0 ^1 e^x x^n dx I_0 =∫_0 ^1 e^x dx=e−1 I_n =[e^x x^n ]_0 ^1 −n∫_0 ^1 e^x x^(n−1) dx I_n =e−nI_(n−1) let I_n =c_n A_n c_n A_n =e−nc_(n−1) A_(n−1) c_n A_n +nc_(n−1) A_(n−1) =e set c_n =−nc_(n−1) , i.e. (c_n /c_(n−1) )=−n (c_n /c_(n−1) )×(c_(n−1) /c_(n−2) )×...×(c_2 /c_1 )×(c_1 /c_0 )=(−1)^n n! (c_n /c_0 )=(−1)^n n! c_n =(−1)^n n!c_0 c_n (A_n −A_(n−1) )=e A_n −A_(n−1) =(e/((−1)^n n!c_0 )) Σ_(n=1) ^m (A_n −A_(n−1) )=Σ_(n=1) ^m (e/((−1)^n n!c_0 )) A_m −A_0 =(e/c_0 )Σ_(n=1) ^m (((−1)^n )/(n!)) A_m =(e/c_0 )Σ_(n=1) ^m (((−1)^n )/(n!))+A_0 c_m A_m =c_m [(e/c_0 )Σ_(n=1) ^m (((−1)^n )/(n!))+A_0 ] I_m =(−1)^m m!c_0 [(e/c_0 )Σ_(n=1) ^m (((−1)^n )/(n!))+(I_0 /c_0 )] I_m =(−1)^m m![eΣ_(n=1) ^m (((−1)^n )/(n!))+I_0 ] I_m =(−1)^m m![eΣ_(n=1) ^m (((−1)^n )/(n!))+e−1] or I_n =(−1)^n n!e[Σ_(k=1) ^n (((−1)^k )/(k!))+1−(1/e)]](https://www.tinkutara.com/question/Q182282.png)
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}} {x}^{{n}} {dx} \\ $$$${I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}} {dx}={e}−\mathrm{1} \\ $$$${I}_{{n}} =\left[{e}^{{x}} {x}^{{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} −{n}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}} {x}^{{n}−\mathrm{1}} {dx} \\ $$$${I}_{{n}} ={e}−{nI}_{{n}−\mathrm{1}} \\ $$$${let}\:{I}_{{n}} ={c}_{{n}} {A}_{{n}} \\ $$$${c}_{{n}} {A}_{{n}} ={e}−{nc}_{{n}−\mathrm{1}} {A}_{{n}−\mathrm{1}} \\ $$$${c}_{{n}} {A}_{{n}} +{nc}_{{n}−\mathrm{1}} {A}_{{n}−\mathrm{1}} ={e} \\ $$$${set}\:{c}_{{n}} =−{nc}_{{n}−\mathrm{1}} ,\:{i}.{e}.\:\frac{{c}_{{n}} }{{c}_{{n}−\mathrm{1}} }=−{n} \\ $$$$\frac{{c}_{{n}} }{{c}_{{n}−\mathrm{1}} }×\frac{{c}_{{n}−\mathrm{1}} }{{c}_{{n}−\mathrm{2}} }×…×\frac{{c}_{\mathrm{2}} }{{c}_{\mathrm{1}} }×\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{0}} }=\left(−\mathrm{1}\right)^{{n}} {n}! \\ $$$$\frac{{c}_{{n}} }{{c}_{\mathrm{0}} }=\left(−\mathrm{1}\right)^{{n}} {n}! \\ $$$${c}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}!{c}_{\mathrm{0}} \\ $$$${c}_{{n}} \left({A}_{{n}} −{A}_{{n}−\mathrm{1}} \right)={e} \\ $$$${A}_{{n}} −{A}_{{n}−\mathrm{1}} =\frac{{e}}{\left(−\mathrm{1}\right)^{{n}} {n}!{c}_{\mathrm{0}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\left({A}_{{n}} −{A}_{{n}−\mathrm{1}} \right)=\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{e}}{\left(−\mathrm{1}\right)^{{n}} {n}!{c}_{\mathrm{0}} } \\ $$$${A}_{{m}} −{A}_{\mathrm{0}} =\frac{{e}}{{c}_{\mathrm{0}} }\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!} \\ $$$${A}_{{m}} =\frac{{e}}{{c}_{\mathrm{0}} }\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}+{A}_{\mathrm{0}} \\ $$$${c}_{{m}} {A}_{{m}} ={c}_{{m}} \left[\frac{{e}}{{c}_{\mathrm{0}} }\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}+{A}_{\mathrm{0}} \right] \\ $$$${I}_{{m}} =\left(−\mathrm{1}\right)^{{m}} {m}!{c}_{\mathrm{0}} \left[\frac{{e}}{{c}_{\mathrm{0}} }\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}+\frac{{I}_{\mathrm{0}} }{{c}_{\mathrm{0}} }\right] \\ $$$${I}_{{m}} =\left(−\mathrm{1}\right)^{{m}} {m}!\left[{e}\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}+{I}_{\mathrm{0}} \right] \\ $$$${I}_{{m}} =\left(−\mathrm{1}\right)^{{m}} {m}!\left[{e}\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}+{e}−\mathrm{1}\right] \\ $$$${or} \\ $$$${I}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}!{e}\left[\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!}+\mathrm{1}−\frac{\mathrm{1}}{{e}}\right] \\ $$
