Question Number 101835 by bobhans last updated on 05/Jul/20
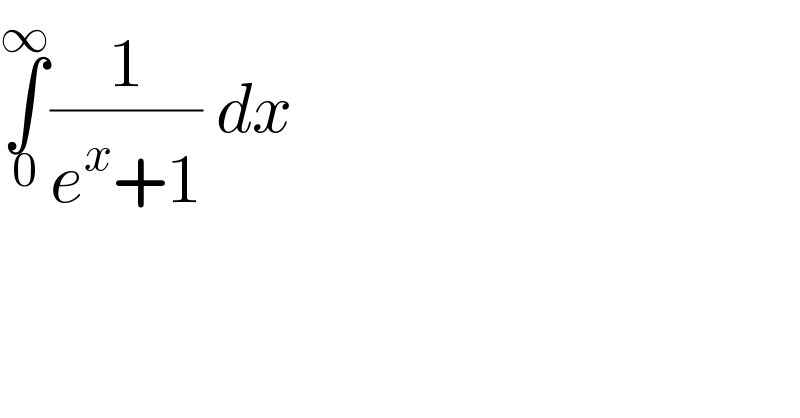
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{{e}^{{x}} +\mathrm{1}}\:{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jul/20
![∫_0 ^∞ (e^x /(e^x (e^x +1)))dx=∫_0 ^∞ (dt/((t−1)t))=∫_2 ^∞ ((1/(t−1))−(1/t))dt=[log(((t−1)/t))]_2 ^∞ =log2 {suppose e^x +1=t](https://www.tinkutara.com/question/Q101861.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{x}} }{{e}^{{x}} \left({e}^{{x}} +\mathrm{1}\right)}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\left({t}−\mathrm{1}\right){t}}=\int_{\mathrm{2}} ^{\infty} \left(\frac{\mathrm{1}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}}\right){dt}=\left[{log}\left(\frac{{t}−\mathrm{1}}{{t}}\right)\right]_{\mathrm{2}} ^{\infty} \\ $$$$={log}\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{suppose}\:{e}^{{x}} +\mathrm{1}={t}\right. \\ $$
Answered by john santu last updated on 05/Jul/20
![set e^x = tan^2 p →dx = ((2sec^2 p dp)/(tan p)) I= 2∫_(π/4) ^(π/2) ((sec^2 p dp)/(tan p(tan^2 p+1))) I = 2∫_(π/4) ^(π/2) cot p dp = 2[ ln ∣sin p∣]_(π/4) ^(π/2) = 2ln(1)−2ln(((√2)/2)) = ln(2) (JS ⊛)](https://www.tinkutara.com/question/Q101837.png)
$${set}\:{e}^{{x}} \:=\:\mathrm{tan}\:^{\mathrm{2}} {p}\:\rightarrow{dx}\:=\:\frac{\mathrm{2sec}\:^{\mathrm{2}} {p}\:{dp}}{\mathrm{tan}\:{p}} \\ $$$${I}=\:\mathrm{2}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} {p}\:{dp}}{\mathrm{tan}\:{p}\left(\mathrm{tan}\:^{\mathrm{2}} {p}+\mathrm{1}\right)} \\ $$$${I}\:=\:\mathrm{2}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{cot}\:{p}\:{dp}\:=\:\mathrm{2}\left[\:\mathrm{ln}\:\mid\mathrm{sin}\:{p}\mid\right]_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \\ $$$$=\:\mathrm{2ln}\left(\mathrm{1}\right)−\mathrm{2ln}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:=\:\mathrm{ln}\left(\mathrm{2}\right)\: \\ $$$$\left(\mathrm{J}{S}\:\circledast\right) \\ $$
Answered by mathmax by abdo last updated on 05/Jul/20
![I =∫_0 ^∞ (dx/(e^x +1)) we do the changement e^x =t ⇒I =∫_1 ^(+∞) (dt/(t(t+1))) =∫_1 ^∞ ((1/t)−(1/(t+1)))dt =[ln∣(t/(t+1))∣]_1 ^∞ =−ln((1/2)) =ln(2)](https://www.tinkutara.com/question/Q101894.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}\:=\left[\mathrm{ln}\mid\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mid\right]_{\mathrm{1}} ^{\infty} \:=−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{ln}\left(\mathrm{2}\right) \\ $$
