Menu Close

0-1-e-x-2-dx-1-1-1-2-3-2-7-10-2-32-42-2-174-216-2-1196-1312-2-

Tinku Tara 0 Comments
Pin




Question Number 129376 by Dwaipayan Shikari last updated on 15/Jan/21
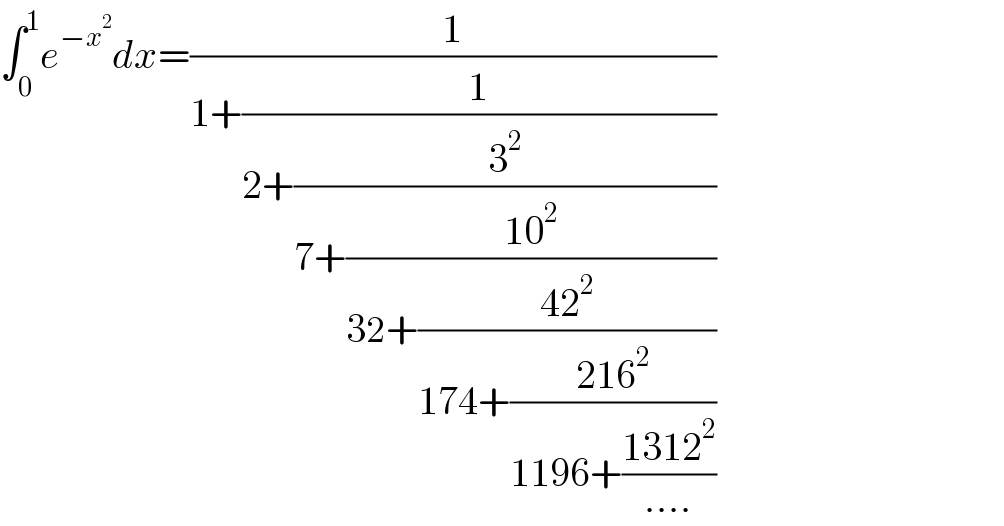
∫_0 ^1 e^(−x^2 ) dx=(1/(1+(1/(2+(3^2 /(7+((10^2 )/(32+((42^2 )/(174+((216^2 )/(1196+((1312^2 )/(....))))))))))))))
$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{7}+\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{32}+\frac{\mathrm{42}^{\mathrm{2}} }{\mathrm{174}+\frac{\mathrm{216}^{\mathrm{2}} }{\mathrm{1196}+\frac{\mathrm{1312}^{\mathrm{2}} }{….}}}}}}} \\ $$
Commented by Dwaipayan Shikari last updated on 15/Jan/21
∫_0 ^a e^(−x^2 ) dx=∫_0 ^a 1−x^2 +(x^4 /(2!))−(x^6 /(3!))+(x^8 /(4!))−... =a−(a^3 /(3.1!))+(a^5 /(5.2!))−(a^7 /(7.3!))+(a^9 /(9.4!))−.. =a+a(−(a^2 /(3.1!)))+a.(((−a^2 )/(3.1!)))(((−3.1!a^2 )/(5.2!)))+a(((−a^2 )/(3.1!)))(−((3.1!a^2 )/(5.2!)))(((−5.2!)/(7.3!))a^2 )+.. =(a/(1+((a^2 /(3.1!))/(1−(a^2 /(3.1!))+(((3.1!a^2 )/(5.2!))/(1−((3.1!a^2 )/(5.2!))+(((5.2!a^2 )/(7.3!))/(1−((5.2!)/(7.3!))a^2 +...)))) )))) =(a/(1+(a^2 /(3.1!−a^2 +(((3.1!)^2 a^2 )/(5.2!−3.1!a^2 +(((5.2!)^2 a^2 )/(7.3!−5.2!a^2 +(7.3!)^2 ...))))))))
$$\int_{\mathrm{0}} ^{{a}} {e}^{−{x}^{\mathrm{2}} } {dx}=\int_{\mathrm{0}} ^{{a}} \mathrm{1}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{8}} }{\mathrm{4}!}−… \\ $$$$={a}−\frac{{a}^{\mathrm{3}} }{\mathrm{3}.\mathrm{1}!}+\frac{{a}^{\mathrm{5}} }{\mathrm{5}.\mathrm{2}!}−\frac{{a}^{\mathrm{7}} }{\mathrm{7}.\mathrm{3}!}+\frac{{a}^{\mathrm{9}} }{\mathrm{9}.\mathrm{4}!}−.. \\ $$$$={a}+{a}\left(−\frac{{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!}\right)+{a}.\left(\frac{−{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!}\right)\left(\frac{−\mathrm{3}.\mathrm{1}!{a}^{\mathrm{2}} }{\mathrm{5}.\mathrm{2}!}\right)+{a}\left(\frac{−{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!}\right)\left(−\frac{\mathrm{3}.\mathrm{1}!{a}^{\mathrm{2}} }{\mathrm{5}.\mathrm{2}!}\right)\left(\frac{−\mathrm{5}.\mathrm{2}!}{\mathrm{7}.\mathrm{3}!}{a}^{\mathrm{2}} \right)+.. \\ $$$$=\frac{{a}}{\mathrm{1}+\frac{\frac{{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!}}{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!}+\frac{\frac{\mathrm{3}.\mathrm{1}!{a}^{\mathrm{2}} }{\mathrm{5}.\mathrm{2}!}}{\mathrm{1}−\frac{\mathrm{3}.\mathrm{1}!{a}^{\mathrm{2}} }{\mathrm{5}.\mathrm{2}!}+\frac{\frac{\mathrm{5}.\mathrm{2}!{a}^{\mathrm{2}} }{\mathrm{7}.\mathrm{3}!}}{\mathrm{1}−\frac{\mathrm{5}.\mathrm{2}!}{\mathrm{7}.\mathrm{3}!}{a}^{\mathrm{2}} +…}}\:}} \\ $$$$=\frac{{a}}{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{\mathrm{3}.\mathrm{1}!−{a}^{\mathrm{2}} +\frac{\left(\mathrm{3}.\mathrm{1}!\right)^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{5}.\mathrm{2}!−\mathrm{3}.\mathrm{1}!{a}^{\mathrm{2}} +\frac{\left(\mathrm{5}.\mathrm{2}!\right)^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{7}.\mathrm{3}!−\mathrm{5}.\mathrm{2}!{a}^{\mathrm{2}} +\left(\mathrm{7}.\mathrm{3}!\right)^{\mathrm{2}} …}}}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *