Question Number 53292 by gunawan last updated on 20/Jan/19

$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx}=.. \\ $$
Commented by maxmathsup by imad last updated on 20/Jan/19
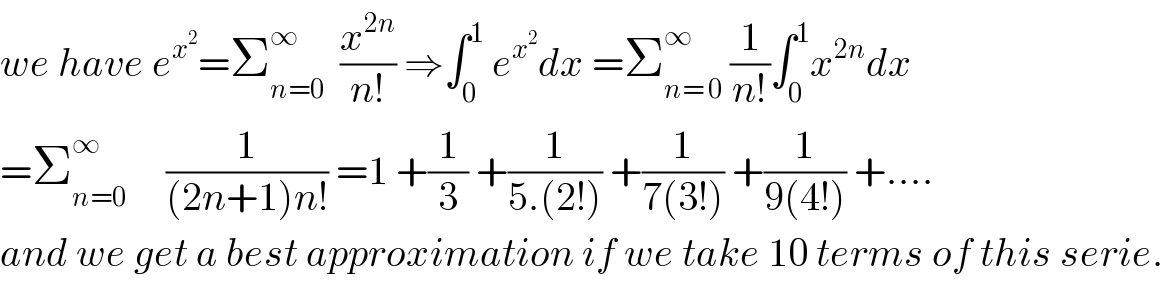
$${we}\:{have}\:{e}^{{x}^{\mathrm{2}} } =\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}{n}} }{{n}!}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{x}^{\mathrm{2}} } {dx}\:=\sum_{{n}=\:\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty\:} \:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\:=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}.\left(\mathrm{2}!\right)}\:+\frac{\mathrm{1}}{\mathrm{7}\left(\mathrm{3}!\right)}\:+\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{4}!\right)}\:+…. \\ $$$${and}\:{we}\:{get}\:{a}\:{best}\:{approximation}\:{if}\:{we}\:{take}\:\mathrm{10}\:{terms}\:{of}\:{this}\:{serie}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19
![aprroximation f(x)=e^x^2 f(0)=1 f(1)=e trapazium area=(1/2)[f(0)+f(1)]×(1−0) =(1/2)×(1+e)×1=((1+e)/2)=1.86 from graph ... 1<∫_0 ^1 e^x^2 dx<1.86](https://www.tinkutara.com/question/Q53301.png)
$${aprroximation} \\ $$$${f}\left({x}\right)={e}^{{x}^{\mathrm{2}} } \:\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:{f}\left(\mathrm{1}\right)={e} \\ $$$${trapazium}\:{area}=\frac{\mathrm{1}}{\mathrm{2}}\left[{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)\right]×\left(\mathrm{1}−\mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{1}+{e}\right)×\mathrm{1}=\frac{\mathrm{1}+{e}}{\mathrm{2}}=\mathrm{1}.\mathrm{86} \\ $$$${from}\:{graph}\:… \\ $$$$\mathrm{1}<\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx}<\mathrm{1}.\mathrm{86} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19

