Question Number 56061 by necx1 last updated on 09/Mar/19

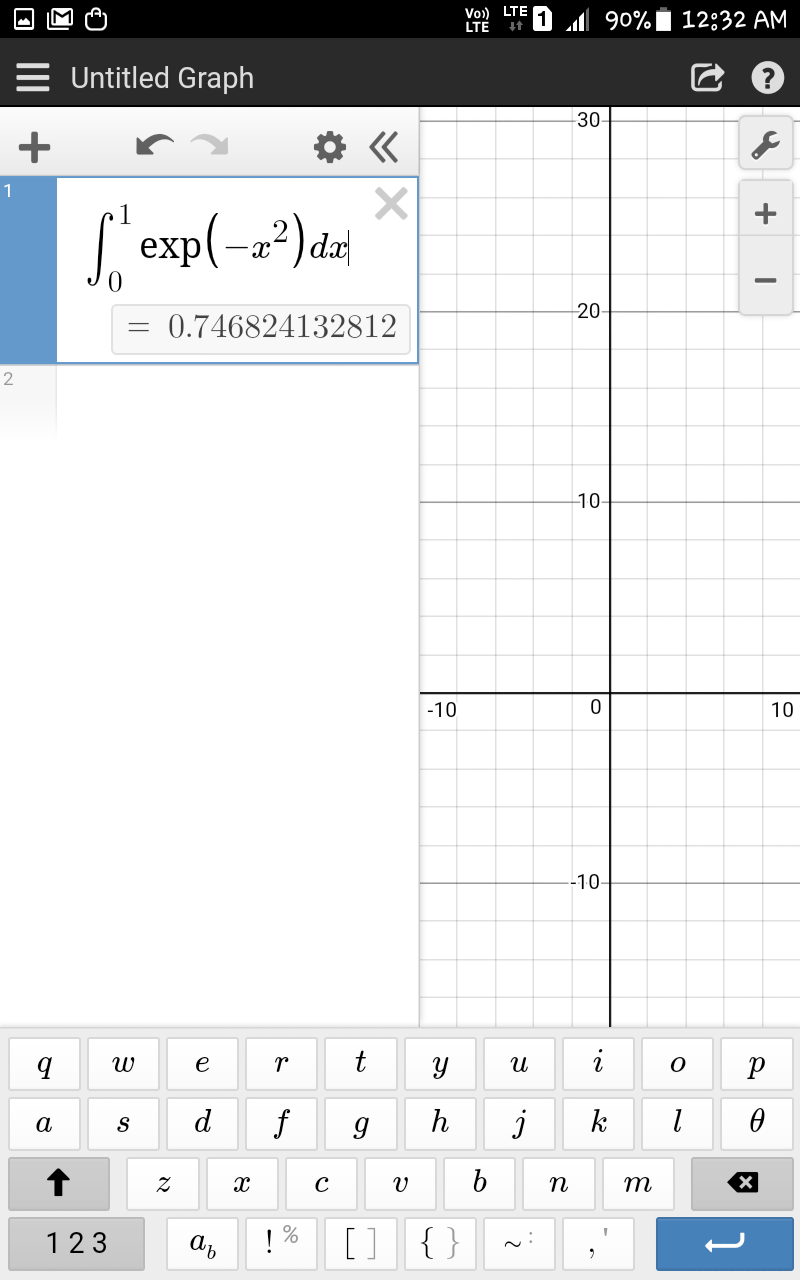
$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}^{\mathrm{2}} } {dx}\:{correct}\:{to}\:\mathrm{3}\:{decimal}\:{place}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Mar/19
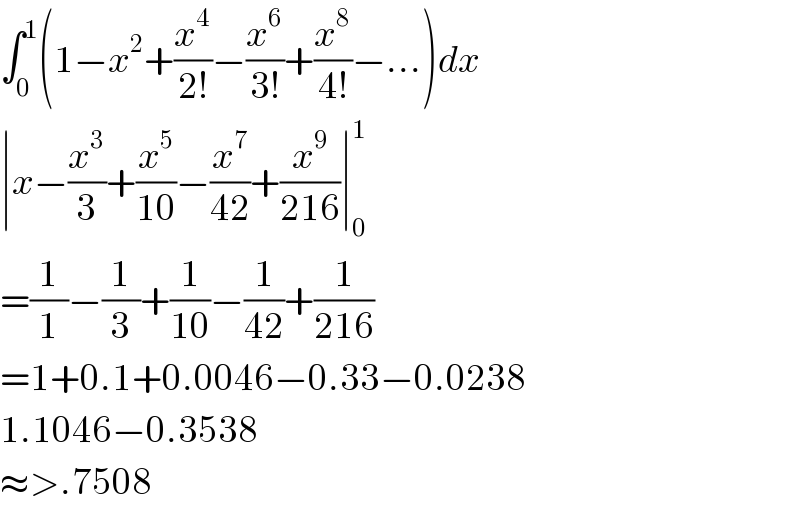
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{8}} }{\mathrm{4}!}−…\right){dx} \\ $$$$\mid{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{10}}−\frac{{x}^{\mathrm{7}} }{\mathrm{42}}+\frac{{x}^{\mathrm{9}} }{\mathrm{216}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{42}}+\frac{\mathrm{1}}{\mathrm{216}} \\ $$$$=\mathrm{1}+\mathrm{0}.\mathrm{1}+\mathrm{0}.\mathrm{0046}−\mathrm{0}.\mathrm{33}−\mathrm{0}.\mathrm{0238} \\ $$$$\mathrm{1}.\mathrm{1046}−\mathrm{0}.\mathrm{3538} \\ $$$$\approx>.\mathrm{7508} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Mar/19
Commented by necx1 last updated on 09/Mar/19
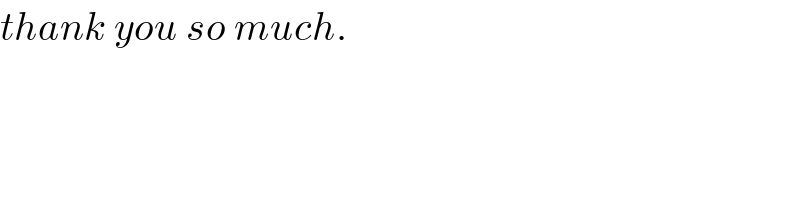
$${thank}\:{you}\:{so}\:{much}. \\ $$
