Question Number 94278 by M±th+et+s last updated on 17/May/20

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{\sqrt{{x}}} }{\:\sqrt{{x}}}{dx} \\ $$
Commented by PRITHWISH SEN 2 last updated on 17/May/20
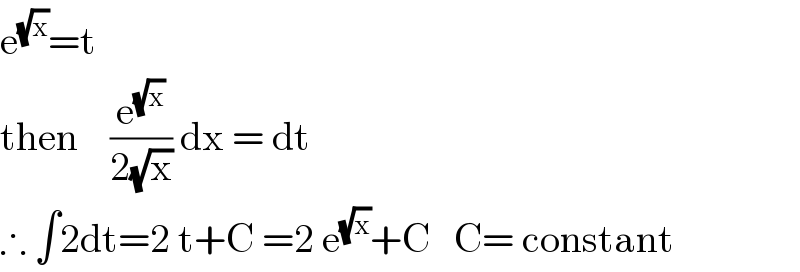
$$\mathrm{e}^{\sqrt{\mathrm{x}}} =\mathrm{t} \\ $$$$\mathrm{then}\:\:\:\:\frac{\mathrm{e}^{\sqrt{\mathrm{x}}} }{\mathrm{2}\sqrt{\mathrm{x}}}\:\mathrm{dx}\:=\:\mathrm{dt} \\ $$$$\therefore\:\int\mathrm{2dt}=\mathrm{2}\:\mathrm{t}+\mathrm{C}\:=\mathrm{2}\:\mathrm{e}^{\sqrt{\mathrm{x}}} +\mathrm{C}\:\:\:\mathrm{C}=\:\mathrm{constant} \\ $$
Commented by M±th+et+s last updated on 17/May/20

$${thanks}\:{sir}\:{but}\:{its}\:\int_{\mathrm{0}} ^{\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 17/May/20
![changement (√x)=t give ∫_0 ^1 (e^(√x) /( (√x)))dx =∫_0 ^1 (e^t /t)(2t)dt =2∫_0 ^1 e^t dt =2[e^t ]_0 ^1 =2(e−1) =2e−2](https://www.tinkutara.com/question/Q94287.png)
$${changement}\:\sqrt{{x}}={t}\:{give}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{e}^{\sqrt{{x}}} }{\:\sqrt{{x}}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{e}^{{t}} }{{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} \:{dt}\:=\mathrm{2}\left[{e}^{{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{2}\left({e}−\mathrm{1}\right)\:=\mathrm{2}{e}−\mathrm{2} \\ $$
Commented by M±th+et+s last updated on 17/May/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 17/May/20
$${you}\:{are}\:{welcome}. \\ $$
