Question Number 157744 by mnjuly1970 last updated on 27/Oct/21
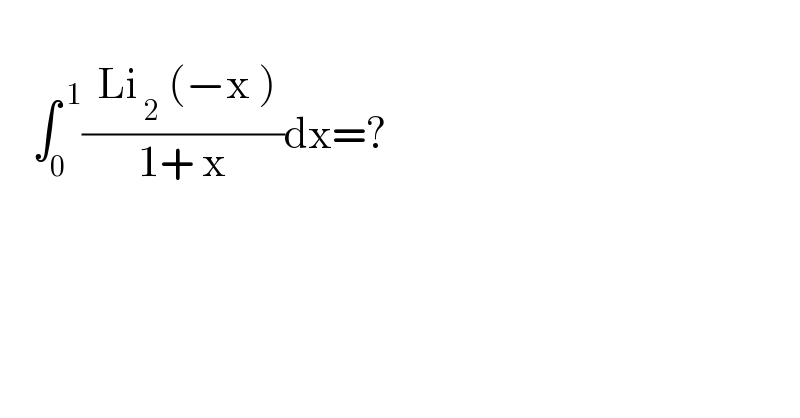
$$ \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\:\mathrm{Li}_{\:\mathrm{2}} \:\left(−\mathrm{x}\:\right)\:}{\mathrm{1}+\:\mathrm{x}}\mathrm{dx}=? \\ $$$$ \\ $$$$ \\ $$
Answered by mindispower last updated on 27/Oct/21
![ln(2)Li_2 (−1)+∫_0 ^1 ((ln(1+x))/x)ln(1+x)dx ∫_0 ^1 ((ln^2 (1+x))/x)dx=∫_0 ^(ln(2)) ((t^2 e^t dt)/(e^t −1))=Ω ∫_0 ^(ln(2)) t^2 e^(−nt) d=((t^2 e^(−nt) )/(−n))+(2/n)∫te^(−nt) =[[−(2/n^2 )t−(2/n^3 ) −(t^2 /n)]e^(−nt) ]_0 ^(ln(2)) =−(2/n^2 )((1/2))^n −(2/n^3 )((1/2))^n −(1/n)((1/2))^n +(2/n^3 ) 𝛀=∫_0 ^(ln(2)) Σ_(n≥0) t^2 e^(−nt) dt=((ln^3 (2))/3)+Σ_(n≥1) (−(2/n^2 )((1/2))^n −(2/n^3 )((1/2))^n −(1/n)((1/2))^n +(2/n^3 )) Ω=((ln^3 (2))/3)−2Li_2 ((1/2))−2Li_3 ((1/2))+ln((1/2))+2ζ(3) ∫_0 ^1 ((Li_2 (−x))/(1+x))dx=ln(2)Li_2 (−1)+((ln^3 (2))/3)−ln(2)−2(Li_2 ((1/2))+Li_3 ((1/2))−ζ(3)) Li_2 ((1/2)),li_2 (−1),Li_3 ((1/2)) has close form [](https://www.tinkutara.com/question/Q157746.png)
$${ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}{dx}=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \frac{{t}^{\mathrm{2}} {e}^{{t}} {dt}}{{e}^{{t}} −\mathrm{1}}=\Omega \\ $$$$\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} {t}^{\mathrm{2}} {e}^{−{nt}} {d}=\frac{{t}^{\mathrm{2}} {e}^{−{nt}} }{−{n}}+\frac{\mathrm{2}}{{n}}\int{te}^{−{nt}} \\ $$$$=\left[\left[−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }{t}−\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\:−\frac{{t}^{\mathrm{2}} }{{n}}\right]{e}^{−{nt}} \right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} =−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{1}}{\boldsymbol{{n}}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\boldsymbol{{n}}} +\frac{\mathrm{2}}{{n}^{\mathrm{3}} } \\ $$$$\boldsymbol{\Omega}=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \underset{{n}\geqslant\mathrm{0}} {\sum}{t}^{\mathrm{2}} {e}^{−{nt}} {dt}=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\frac{\mathrm{2}}{{n}^{\mathrm{3}} }\right) \\ $$$$\Omega=\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}−\mathrm{2}{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\zeta\left(\mathrm{3}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Li}_{\mathrm{2}} \left(−{x}\right)}{\mathrm{1}+{x}}{dx}={ln}\left(\mathrm{2}\right){Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\frac{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}−{ln}\left(\mathrm{2}\right)−\mathrm{2}\left({Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\zeta\left(\mathrm{3}\right)\right) \\ $$$${Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right),{li}_{\mathrm{2}} \left(−\mathrm{1}\right),{Li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{has}\:{close}\:{form} \\ $$$$ \\ $$$$\left[\right. \\ $$
Commented by mnjuly1970 last updated on 27/Oct/21
$$\:\:\:\:\:\:\:\:\:\:\:\:\:{thanks}\:{alot}\:{sir}\:{power}….. \\ $$
Commented by mindispower last updated on 27/Oct/21

$${withe}\:{pleasur}\:{God}\:{bless}\:{You} \\ $$
