Question Number 163682 by mnjuly1970 last updated on 09/Jan/22
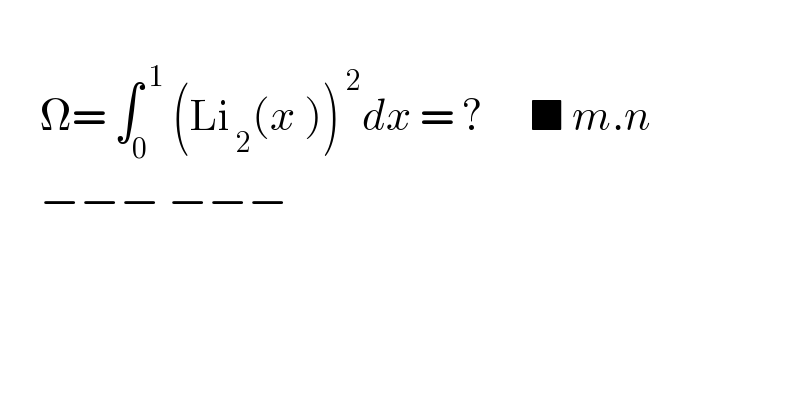
$$ \\ $$$$\:\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\left(\mathrm{Li}_{\:\mathrm{2}} ^{\:} \left({x}\:\right)\right)^{\:\mathrm{2}} {dx}\:=\:?\:\:\:\:\:\:\blacksquare\:{m}.{n}\:\:\: \\ $$$$\:\:\:\:\:−−−\:−−− \\ $$$$\:\:\:\: \\ $$
Answered by Kamel last updated on 09/Jan/22
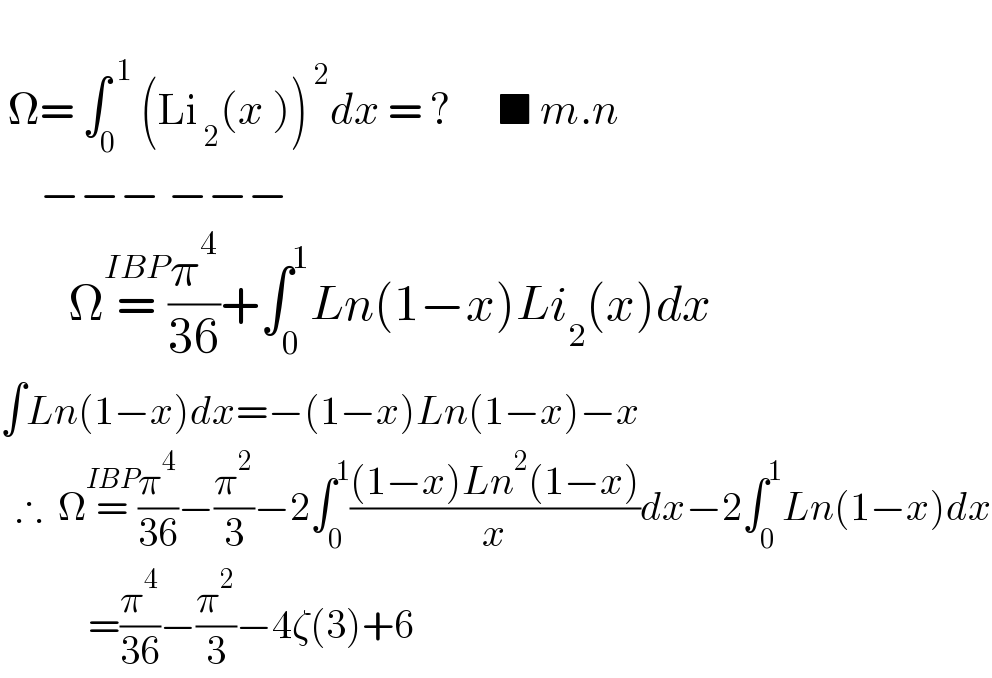
$$ \\ $$$$\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\left(\mathrm{Li}_{\:\mathrm{2}} ^{\:} \left({x}\:\right)\right)^{\:\mathrm{2}} {dx}\:=\:?\:\:\:\:\:\:\blacksquare\:{m}.{n}\:\:\: \\ $$$$\:\:\:\:\:−−−\:−−− \\ $$$$\:\:\:\:\:\:\:\Omega\overset{{IBP}} {=}\frac{\pi^{\mathrm{4}} }{\mathrm{36}}+\int_{\mathrm{0}} ^{\mathrm{1}} {Ln}\left(\mathrm{1}−{x}\right){Li}_{\mathrm{2}} \left({x}\right){dx}\: \\ $$$$\int{Ln}\left(\mathrm{1}−{x}\right){dx}=−\left(\mathrm{1}−{x}\right){Ln}\left(\mathrm{1}−{x}\right)−{x} \\ $$$$\:\:\therefore\:\:\Omega\overset{{IBP}} {=}\frac{\pi^{\mathrm{4}} }{\mathrm{36}}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right){Ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{{x}}{dx}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {Ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\pi^{\mathrm{4}} }{\mathrm{36}}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{4}\zeta\left(\mathrm{3}\right)+\mathrm{6} \\ $$
Commented by mnjuly1970 last updated on 09/Jan/22
$$\:\:\:\:{very}\:{nice}\:{sir}\:{kamel} \\ $$
