Question Number 147195 by mnjuly1970 last updated on 18/Jul/21

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{Li}_{\:\mathrm{2}} \left(\:\sqrt{{x}}\:\right){dx}\:=\:? \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 18/Jul/21
![Ω = ∫_0 ^1 Li_2 ((√x)) dx Ω = ∫_0 ^1 Σ_(k=1) ^∞ ((((√x))^k )/k^2 ) dx Ω = ∫_0 ^1 Σ_(k=1) ^∞ (x^(k/2) /k^2 ) dx Ω = [Σ_(k=1) ^∞ (x^((k/2)+1) /(k^2 ((k/2)+1)))]_0 ^1 Ω = Σ_(k=1) ^∞ (1/(k^2 ((k/2)+1))) Ω = 2Σ_(k=1) ^∞ (1/(k^2 (k+2))) Ω = Σ_(k=1) ^∞ ((1/k^2 )−(1/2).(1/k)+(1/2).(1/(k+2))) Ω = Σ_(k=1) ^∞ (1/k^2 )−(1/2)Σ_(k=1) ^∞ ((1/k)−(1/(k+2))) Ω = (π^2 /6)−(1/2)(1+(1/2)) Ω = (π^2 /6)−(3/4)](https://www.tinkutara.com/question/Q147210.png)
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left(\sqrt{{x}}\right)\:{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\sqrt{{x}}\right)^{{k}} }{{k}^{\mathrm{2}} }\:{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\frac{{k}}{\mathrm{2}}} }{{k}^{\mathrm{2}} }\:{dx} \\ $$$$\Omega\:=\:\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\frac{{k}}{\mathrm{2}}+\mathrm{1}} }{{k}^{\mathrm{2}} \left(\frac{{k}}{\mathrm{2}}+\mathrm{1}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left(\frac{{k}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\Omega\:=\:\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{2}\right)} \\ $$$$\Omega\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{{k}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{{k}+\mathrm{2}}\right) \\ $$$$\Omega\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{2}}\right) \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Omega\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/21
$$\:\:\:\:\:{mercey}\:−{thanks}\:{alot}\:{master} \\ $$$$\:\:\:{olaf}\:…. \\ $$
Answered by Kamel last updated on 18/Jul/21
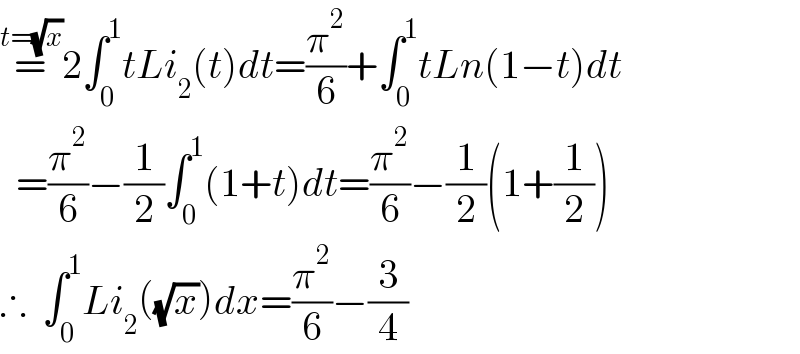
$$\overset{{t}=\sqrt{{x}}} {=}\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {tLi}_{\mathrm{2}} \left({t}\right){dt}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\int_{\mathrm{0}} ^{\mathrm{1}} {tLn}\left(\mathrm{1}−{t}\right){dt} \\ $$$$\:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{t}\right){dt}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\therefore\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {Li}_{\mathrm{2}} \left(\sqrt{{x}}\right){dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/21
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{kamel}.. \\ $$
