Question Number 122963 by Lordose last updated on 21/Nov/20
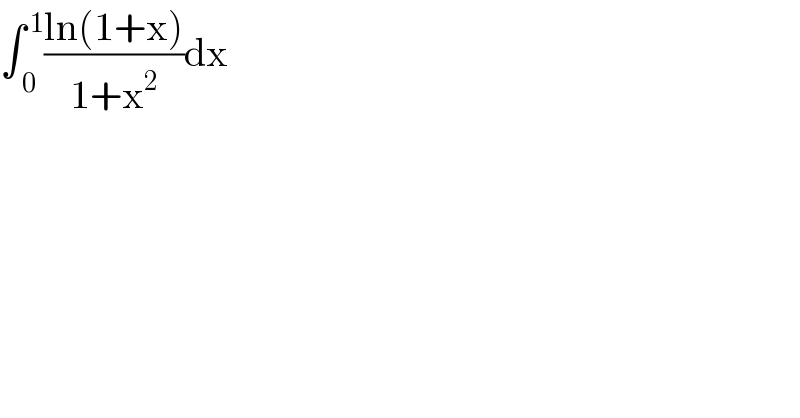
$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Nov/20
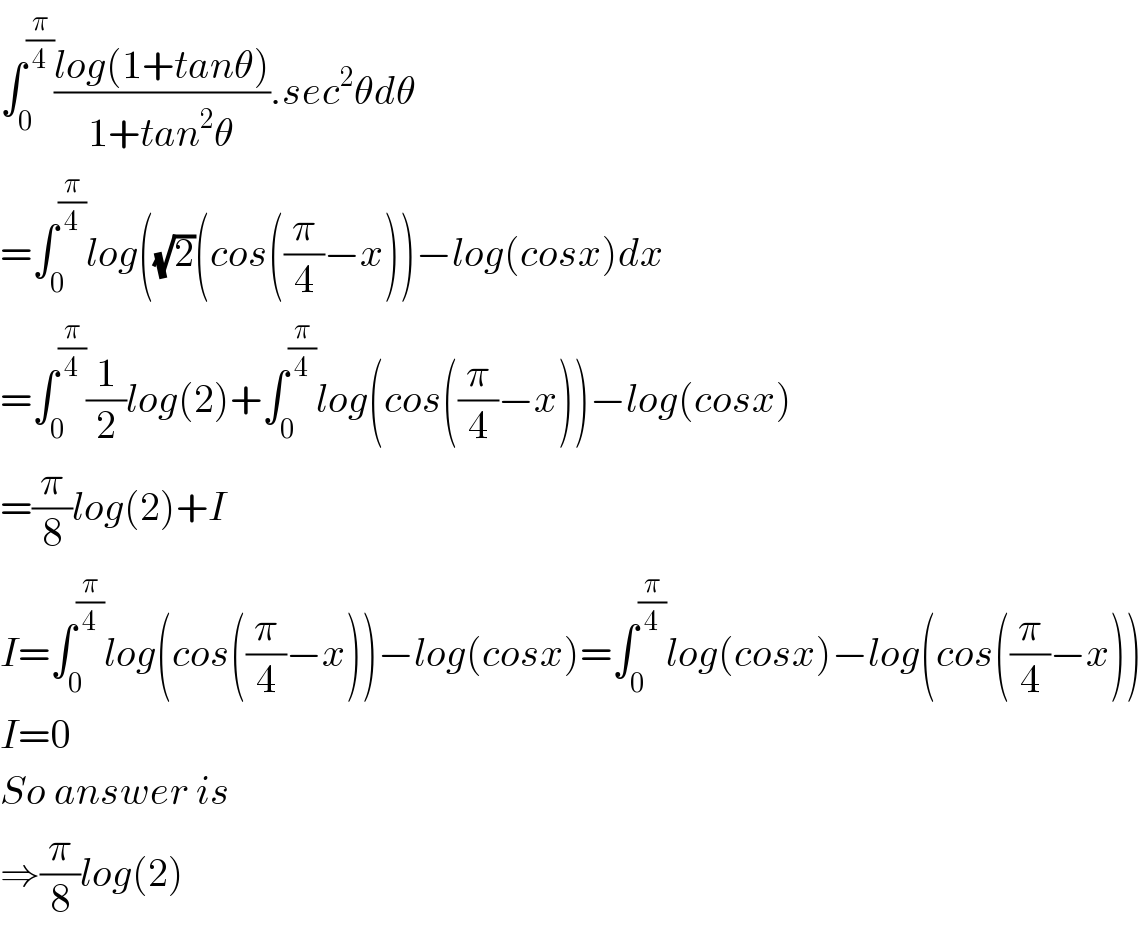
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{log}\left(\mathrm{1}+{tan}\theta\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}.{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\sqrt{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)−{log}\left({cosx}\right){dx}\right. \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)−{log}\left({cosx}\right) \\ $$$$=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right)+{I} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)−{log}\left({cosx}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cosx}\right)−{log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right) \\ $$$${I}=\mathrm{0} \\ $$$${So}\:{answer}\:{is}\: \\ $$$$\Rightarrow\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right) \\ $$
Answered by mnjuly1970 last updated on 21/Nov/20
![solution: x=tan(y)⇒ dx= (1+tan^2 (y))dy I =∫_0 ^( 1) ((ln(1+x))/(1+x^2 ))dx=∫_0 ^( (π/4)) ln(1+tan(y))dy =∫_0 ^( (π/4)) ln[1+tan((π/4)−y)]dy =∫_0 ^( (π/4)) ln(1+((1−tan(y))/(1+tan(y))))dy =∫_0 ^( (π/4)) {ln(2)−ln(1+tan(y))}dy =(π/4)ln(2)−I 2I=(π/4)ln(2) ⇒I=(π/8)ln(2) ✓](https://www.tinkutara.com/question/Q122966.png)
$$\:\:{solution}: \\ $$$$\:\:{x}={tan}\left({y}\right)\Rightarrow\:{dx}=\:\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({y}\right)\right){dy} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tan}\left({y}\right)\right){dy} \\ $$$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left[\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{y}\right)\right]{dy} \\ $$$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tan}\left({y}\right)}{\mathrm{1}+{tan}\left({y}\right)}\right){dy} \\ $$$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \left\{{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{1}+{tan}\left({y}\right)\right)\right\}{dy} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−{I} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\Rightarrow{I}=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:\:\checkmark \\ $$
