Menu Close

0-1-ln-1-x-2-1-x-2-dx-proof-0-1-ln-1-x-1-x-2-dx-pi-8-ln-2-I-0-1-ln-1-x-1-x-2-dx-x-tan

Tinku Tara 0 Comments
Pin




Question Number 156864 by mnjuly1970 last updated on 16/Oct/21
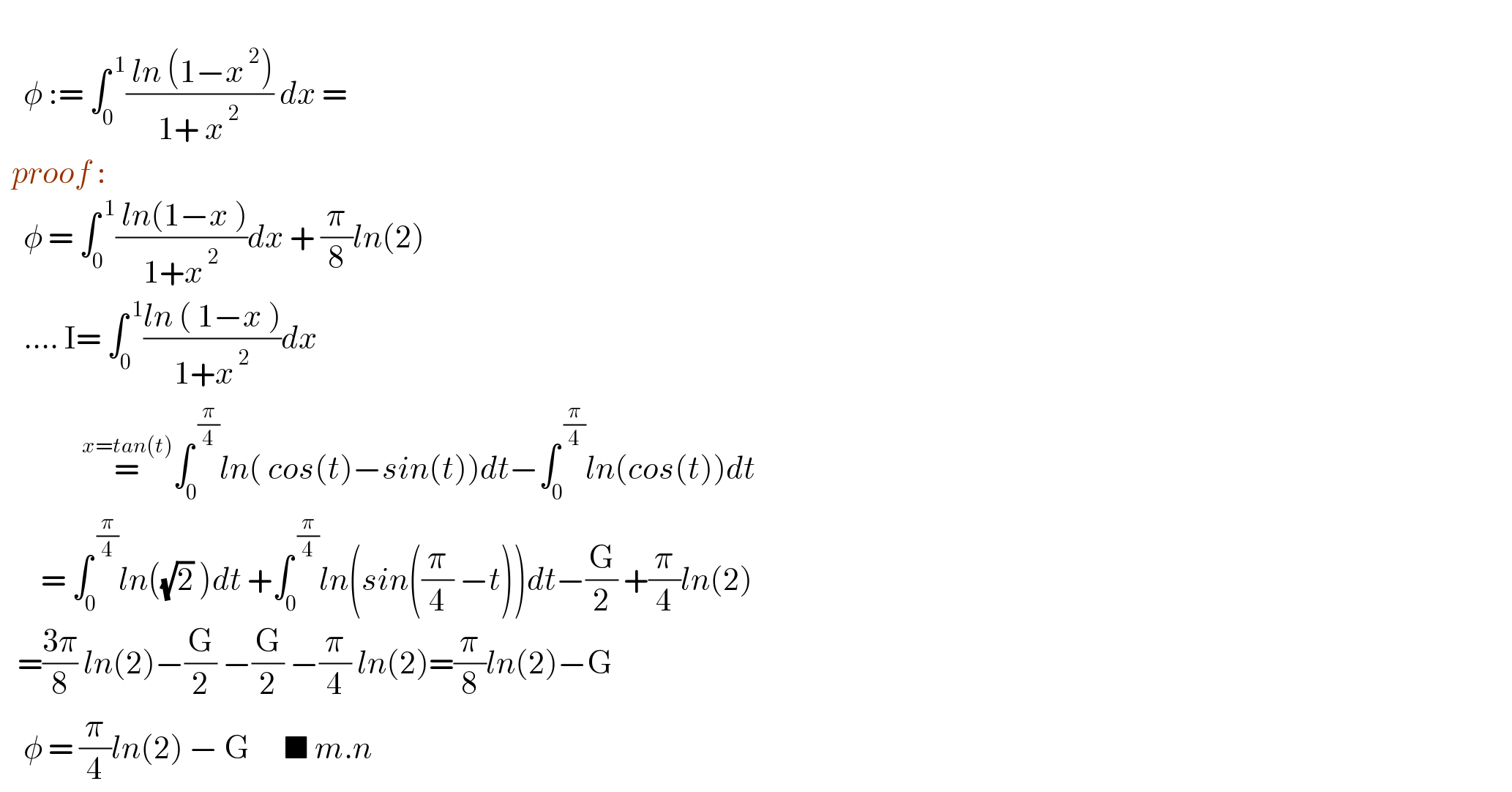
φ := ∫_0 ^( 1) (( ln (1−x^( 2) ))/(1+ x^( 2) )) dx = proof : φ = ∫_0 ^( 1) (( ln(1−x ))/(1+x^( 2) ))dx + (π/8)ln(2) .... I= ∫_0 ^( 1) ((ln ( 1−x ))/(1+x^( 2) ))dx =^(x=tan(t)) ∫_0 ^( (π/4)) ln( cos(t)−sin(t))dt−∫_0 ^( (π/4)) ln(cos(t))dt = ∫_0 ^( (π/4)) ln((√2) )dt +∫_0 ^( (π/4)) ln(sin((π/4) −t))dt−(G/2) +(π/4)ln(2) =((3π)/8) ln(2)−(G/2) −(G/2) −(π/4) ln(2)=(π/8)ln(2)−G φ = (π/4)ln(2) − G ■ m.n
$$ \\ $$$$\:\:\:\:\phi\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{ln}\:\left(\mathrm{1}−{x}^{\:\mathrm{2}} \right)}{\mathrm{1}+\:{x}^{\:\mathrm{2}} }\:{dx}\:= \\ $$$$\:\:{proof}\:: \\ $$$$\:\:\:\:\phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{ln}\left(\mathrm{1}−{x}\:\right)}{\mathrm{1}+{x}^{\:\mathrm{2}} }{dx}\:+\:\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:….\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\:\left(\:\mathrm{1}−{x}\:\right)}{\mathrm{1}+{x}^{\:\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{{x}={tan}\left({t}\right)} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\:{cos}\left({t}\right)−{sin}\left({t}\right)\right){dt}−\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$$\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}\:\right){dt}\:+\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left(\frac{\pi}{\mathrm{4}}\:−{t}\right)\right){dt}−\frac{\mathrm{G}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:=\frac{\mathrm{3}\pi}{\mathrm{8}}\:{ln}\left(\mathrm{2}\right)−\frac{\mathrm{G}}{\mathrm{2}}\:−\frac{\mathrm{G}}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\:{ln}\left(\mathrm{2}\right)=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)−\mathrm{G} \\ $$$$\:\:\:\:\phi\:=\:\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:−\:\mathrm{G}\:\:\:\:\:\:\blacksquare\:{m}.{n} \\ $$
Commented by mnjuly1970 last updated on 16/Oct/21
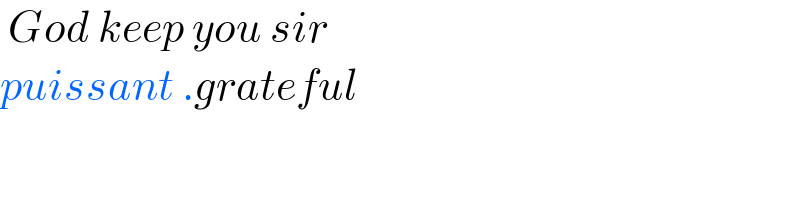
God keep you sir puissant .grateful
$$\:{God}\:{keep}\:{you}\:{sir} \\ $$$${puissant}\:.{grateful} \\ $$
Commented by puissant last updated on 16/Oct/21
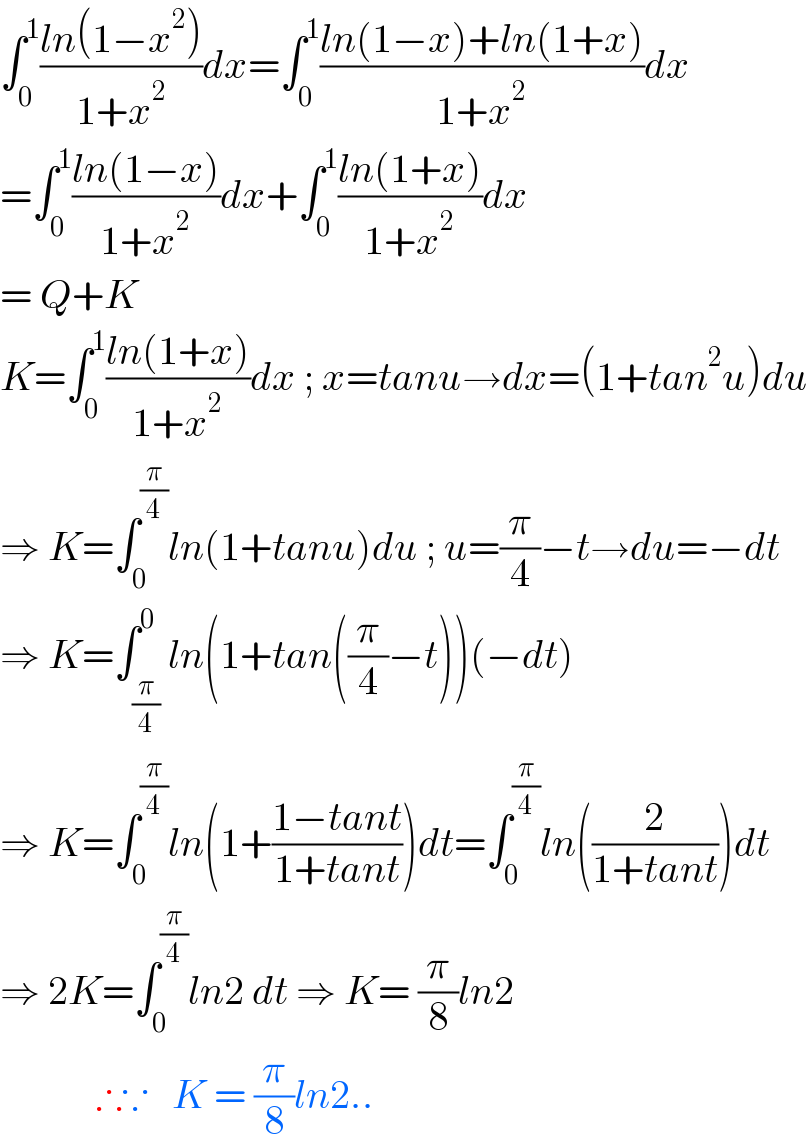
∫_0 ^1 ((ln(1−x^2 ))/(1+x^2 ))dx=∫_0 ^1 ((ln(1−x)+ln(1+x))/(1+x^2 ))dx =∫_0 ^1 ((ln(1−x))/(1+x^2 ))dx+∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx = Q+K K=∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx ; x=tanu→dx=(1+tan^2 u)du ⇒ K=∫_0 ^(π/4) ln(1+tanu)du ; u=(π/4)−t→du=−dt ⇒ K=∫_(π/4) ^0 ln(1+tan((π/4)−t))(−dt) ⇒ K=∫_0 ^(π/4) ln(1+((1−tant)/(1+tant)))dt=∫_0 ^(π/4) ln((2/(1+tant)))dt ⇒ 2K=∫_0 ^(π/4) ln2 dt ⇒ K= (π/8)ln2 ∴∵ K = (π/8)ln2..
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)+{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\:{Q}+{K} \\ $$$${K}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:;\:{x}={tanu}\rightarrow{dx}=\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right){du} \\ $$$$\Rightarrow\:{K}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanu}\right){du}\:;\:{u}=\frac{\pi}{\mathrm{4}}−{t}\rightarrow{du}=−{dt} \\ $$$$\Rightarrow\:{K}=\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} {ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right)\left(−{dt}\right) \\ $$$$\Rightarrow\:{K}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tant}}{\mathrm{1}+{tant}}\right){dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tant}}\right){dt} \\ $$$$\Rightarrow\:\mathrm{2}{K}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}\:{dt}\:\Rightarrow\:{K}=\:\frac{\pi}{\mathrm{8}}{ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:\:{K}\:=\:\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}.. \\ $$
Commented by puissant last updated on 16/Oct/21
Great , Good sir Mnjuly1970.
$${Great}\:,\:{Good}\:{sir}\:{Mnjuly}\mathrm{1970}. \\ $$
Commented by mnjuly1970 last updated on 16/Oct/21
thanks alot ...
$${thanks}\:{alot}\:… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *