Question Number 163759 by amin96 last updated on 10/Jan/22
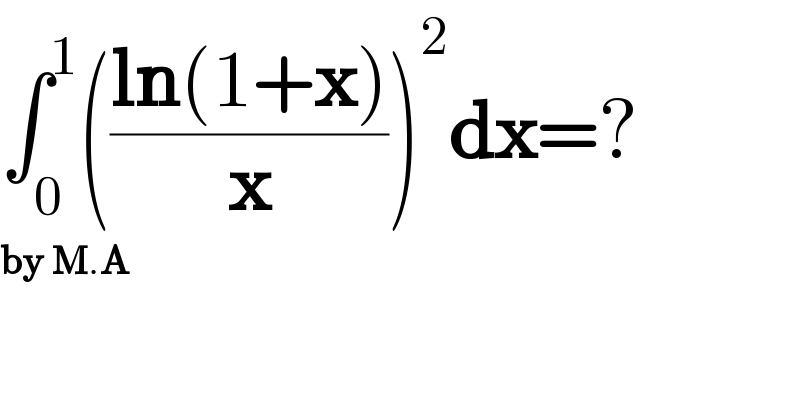
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{2}} \boldsymbol{\mathrm{dx}}=? \\ $$$$\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{M}}.\boldsymbol{\mathrm{A}} \\ $$
Answered by Kamel last updated on 10/Jan/22
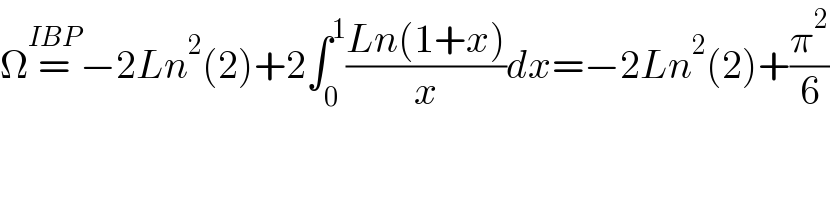
$$\Omega\overset{{IBP}} {=}−\mathrm{2}{Ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}=−\mathrm{2}{Ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Answered by mathmax by abdo last updated on 11/Jan/22
![Υ=∫_0 ^1 ((ln^2 (1+x))/x^2 )dx ⇒Υ=[−(1/x)ln^2 (1+x)]_0 ^1 +∫_0 ^1 (1/x)×((2ln(1+x))/(1+x))dx =−ln^2 (2)+2∫_0 ^1 ((ln(1+x))/(x(1+x)))dx and ∫_0 ^1 ((ln(1+x))/(x(1+x)))dx=∫_0 ^1 ((1/x)−(1/(x+1)))ln(1+x)dx =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 ((ln(1+x))/(1+x))dx we have ln^′ (1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) ⇒∫_0 ^1 ((ln(1+x))/x)dx=∫_0 ^1 Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^(n−1) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)[(x^n /n)]_0 ^1 =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )=−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−δ(2)=−(2^(1−2) −1)ξ(2)=(π^2 /(12)) ∫_0 ^1 ((ln(1+x))/(1+x))dx =_(1+x=t) ∫_1 ^2 ((lnt)/t)dt =(1/2)ln^2 t]_1 ^2 =(1/2)ln^2 2 ⇒ ∫_0 ^1 (((ln(1+x))/x))^2 dx=(π^2 /(12))−((ln^2 2)/2)](https://www.tinkutara.com/question/Q163809.png)
$$\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\Upsilon=\left[−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}}×\frac{\mathrm{2ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\mathrm{dx}\:\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\delta\left(\mathrm{2}\right)=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\left.\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=_{\mathrm{1}+\mathrm{x}=\mathrm{t}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{lnt}}{\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{t}\right]_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \mathrm{2}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\right)^{\mathrm{2}} \mathrm{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{2}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 11/Jan/22
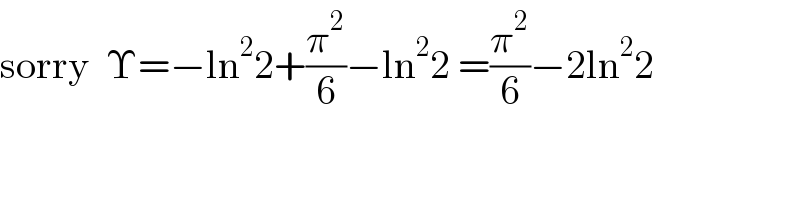
$$\mathrm{sorry}\:\:\Upsilon=−\mathrm{ln}^{\mathrm{2}} \mathrm{2}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{ln}^{\mathrm{2}} \mathrm{2}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{2ln}^{\mathrm{2}} \mathrm{2} \\ $$
Answered by mnjuly1970 last updated on 11/Jan/22
![Ω=^(i.b.p) [−((ln^( 2) (1+x))/x) ]_0 ^( 1) + 2∫_0 ^( 1) (( ln(1+x))/(x( 1+x)))dx = −ln^( 2) (2) +2{∫_0 ^( 1) ((ln(1+x))/x) −∫_0 ^( 1) ((ln(1+x))/(1+x)) dx} = −ln^( 2) (2)−2li_( 2) (−1) −ln^( 2) (2) = 2 η (2 )−3ln^( 2) (2) = ζ (2) −2ln^( 2) (2) ■ m.n](https://www.tinkutara.com/question/Q163841.png)
$$ \\ $$$$\:\:\Omega\overset{{i}.{b}.{p}} {=}\:\left[−\frac{{ln}^{\:\mathrm{2}} \left(\mathrm{1}+{x}\right)}{{x}}\:\right]_{\mathrm{0}} ^{\:\mathrm{1}} +\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{ln}\left(\mathrm{1}+{x}\right)}{{x}\left(\:\mathrm{1}+{x}\right)}{dx} \\ $$$$\:\:\:\:\:\:=\:−{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right)\:+\mathrm{2}\left\{\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}\:{dx}\right\} \\ $$$$\:\:\:\:\:\:\:=\:−{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{2}{li}_{\:\mathrm{2}} \:\left(−\mathrm{1}\right)\:−{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:=\:\:\mathrm{2}\:\eta\:\left(\mathrm{2}\:\right)−\mathrm{3}{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:=\:\zeta\:\left(\mathrm{2}\right)\:−\mathrm{2}{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right)\:\blacksquare\:{m}.{n} \\ $$$$\: \\ $$
