Question Number 130907 by greg_ed last updated on 30/Jan/21
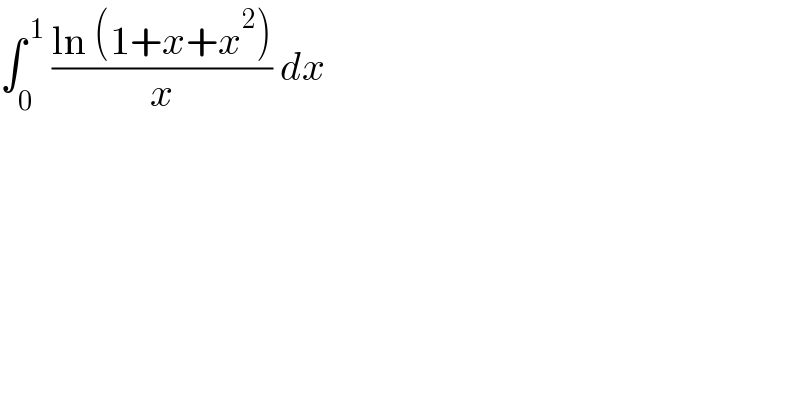
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)}{{x}}\:{dx} \\ $$
Commented by benjo_mathlover last updated on 30/Jan/21
այս հարցն արդեն պատասխանվել է
Commented by benjo_mathlover last updated on 30/Jan/21

$$\mathrm{qn}\:\mathrm{130676} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jan/21
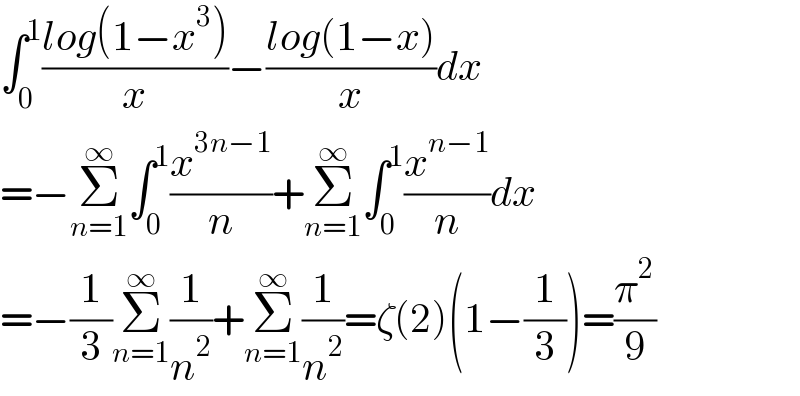
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}^{\mathrm{3}} \right)}{{x}}−\frac{{log}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}{n}−\mathrm{1}} }{{n}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}−\mathrm{1}} }{{n}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\zeta\left(\mathrm{2}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{9}} \\ $$
