Question Number 161967 by amin96 last updated on 24/Dec/21

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}{\left(\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)}\boldsymbol{\mathrm{dx}}=? \\ $$
Answered by phanphuoc last updated on 25/Dec/21
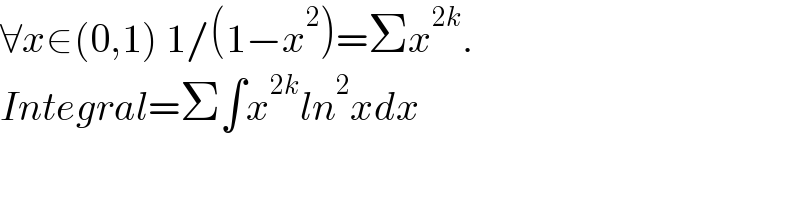
$$\forall{x}\in\left(\mathrm{0},\mathrm{1}\right)\:\mathrm{1}/\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\Sigma{x}^{\mathrm{2}{k}} . \\ $$$${Integral}=\Sigma\int{x}^{\mathrm{2}{k}} {ln}^{\mathrm{2}} {xdx} \\ $$
Answered by Ar Brandon last updated on 25/Dec/21
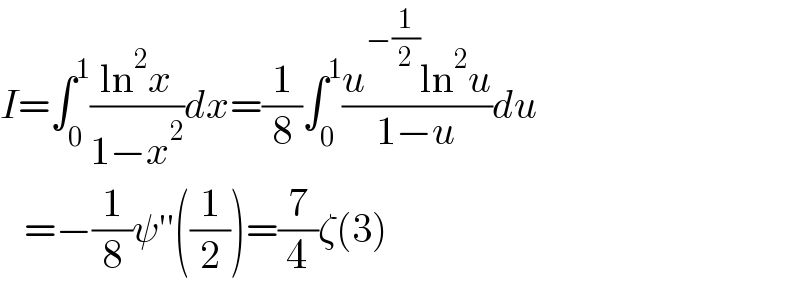
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} {x}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} {u}}{\mathrm{1}−{u}}{du} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{8}}\psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$
Answered by mathmax by abdo last updated on 25/Dec/21
![Υ=∫_0 ^1 ((log^2 x)/(1−x^2 ))dx ⇒Υ=∫_0 ^1 log^2 x(Σ_(n=0) ^∞ x^(2n) )dx =Σ_(n=0) ^∞ ∫_0 ^1 x^(2n) log^2 xdx =Σ_(n=0) ^∞ A_n A_n =∫_0 ^1 x^(2n) log^2 xdx=[(1/(2n+1))x^(2n+1) log^2 x]_0 ^1 −∫_0 ^1 (x^(2n+1) /(2n+1))((2logx)/x)dx =−(2/(2n+1)) ∫_0 ^1 x^(2n) logx dx =−(2/(2n+1)){[ (x^(2n+1) /(2n+1))logx]_0 ^1 −∫_0 ^1 (x^(2n+1) /(2n+1))(dx/x)} =−(2/(2n+1)){−(1/(2n+1))∫_0 ^1 x^(2n) dx =(2/((2n+1)^2 ))×(1/((2n+1)))=(2/((2n+1)^3 )) ⇒ Υ=2Σ_(n=0) ^∞ (1/((2n+1)^3 )) on ξ(3)=Σ_(n=1) ^∞ (1/n^3 )=(1/8)Σ_(n=1) ^∞ (1/n^3 )+Σ_(n=0) ^∞ (1/((2n+1)^3 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^3 ))=(1−(1/8))ξ(3)=(7/8)ξ(3) ⇒ Υ=(7/4)ξ(3)](https://www.tinkutara.com/question/Q162006.png)
$$\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}^{\mathrm{2}} \mathrm{x}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \:\mathrm{log}^{\mathrm{2}} \mathrm{xdx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{A}_{\mathrm{n}} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{log}^{\mathrm{2}} \mathrm{xdx}=\left[\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \mathrm{log}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\frac{\mathrm{2logx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{logx}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\left\{\left[\:\:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\frac{\mathrm{dx}}{\mathrm{x}}\right\} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\left\{−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{dx}\right. \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)}=\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\Upsilon=\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\mathrm{on}\:\xi\left(\mathrm{3}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{8}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)\xi\left(\mathrm{3}\right)=\frac{\mathrm{7}}{\mathrm{8}}\xi\left(\mathrm{3}\right)\:\Rightarrow \\ $$$$\Upsilon=\frac{\mathrm{7}}{\mathrm{4}}\xi\left(\mathrm{3}\right) \\ $$
