Question Number 162177 by mnjuly1970 last updated on 27/Dec/21
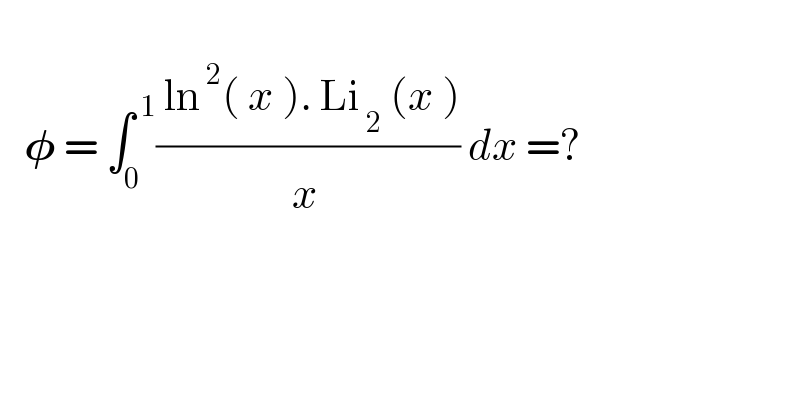
$$ \\ $$$$\:\:\:\boldsymbol{\phi}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{ln}^{\:\mathrm{2}} \left(\:{x}\:\right).\:\mathrm{Li}_{\:\mathrm{2}} \:\left({x}\:\right)}{{x}^{\:} }\:{dx}\:=? \\ $$
Answered by Ar Brandon last updated on 27/Dec/21
![Ο=β«_0 ^1 ((log^2 xLi_2 (x))/x)dx=Ξ£_(n=1) ^β (1/n^2 )β«_0 ^1 ((x^n log^2 x)/x)dx =Ξ£_(n=1) ^β (1/n^2 )([(1/3)x^n log^3 x]_0 ^1 β(n/3)β«_0 ^1 x^(nβ1) log^3 xdx) =β(1/3)Ξ£_(n=1) ^β (1/n)β(β^3 /βΞ±^3 )β£_(Ξ±=nβ1) β«_0 ^1 x^Ξ± dx =β(1/3)Ξ£_(n=1) ^β (1/n)β(β^3 /βΞ±^3 )β£_(Ξ±=nβ1) (1/(Ξ±+1)) =β(1/3)Ξ£_(n=1) ^β (1/n)(((β6)/n^4 ))=2Ξ£_(n=1) ^β (1/n^5 )=2ΞΆ(5)](https://www.tinkutara.com/question/Q162180.png)
$$\phi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}^{\mathrm{2}} {xLi}_{\mathrm{2}} \left({x}\right)}{{x}}{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} {log}^{\mathrm{2}} {x}}{{x}}{dx} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\left[\frac{\mathrm{1}}{\mathrm{3}}{x}^{{n}} {log}^{\mathrm{3}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{{n}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}β\mathrm{1}} {log}^{\mathrm{3}} {xdx}\right) \\ $$$$\:\:\:=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\centerdot\frac{\partial^{\mathrm{3}} }{\partial\alpha^{\mathrm{3}} }\mid_{\alpha={n}β\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\alpha} {dx} \\ $$$$\:\:\:=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\centerdot\frac{\partial^{\mathrm{3}} }{\partial\alpha^{\mathrm{3}} }\mid_{\alpha={n}β\mathrm{1}} \frac{\mathrm{1}}{\alpha+\mathrm{1}} \\ $$$$\:\:\:=β\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\left(\frac{β\mathrm{6}}{{n}^{\mathrm{4}} }\right)=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{5}} }=\mathrm{2}\zeta\left(\mathrm{5}\right) \\ $$
Commented by mnjuly1970 last updated on 27/Dec/21
$$\:{grateful}\:{sir}\:{brandon} \\ $$
Commented by Ar Brandon last updated on 27/Dec/21
$$\mathrm{My}\:\mathrm{pleasure},\:\mathrm{Sir}. \\ $$