Menu Close

0-1-ln-2-x-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 98016 by bemath last updated on 11/Jun/20
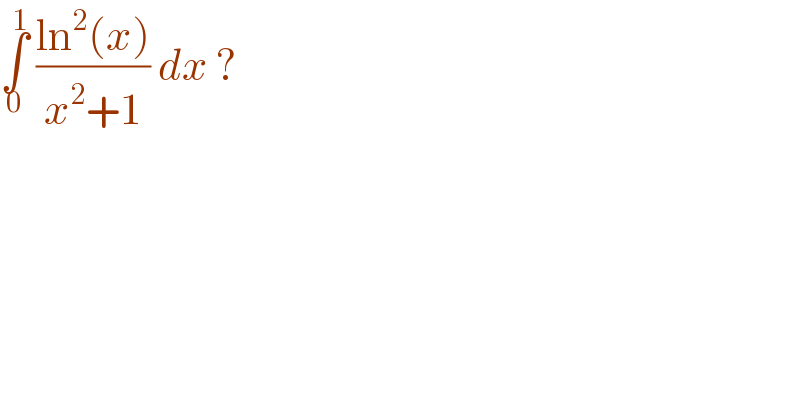
∫_0 ^1 ((ln^2 (x))/(x^2 +1)) dx ?
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{ln}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:?\: \\ $$
Commented by bobhans last updated on 11/Jun/20
substitution w = −ln (x) , x = e^(−w) I= ∫_∞ ^0 (((−w)^2 )/(1+(e^(−w) )^2 )) (−e^(−w) dw) I= ∫_0 ^∞ w^2 .(e^(−w) /(1+e^(−2w) )) dw [ (e^(−w) /(1+e^(−2w) )) = Σ_(n =0) ^∞ (−1)^(n−1) e^(−(2n+1)w) ] I= Σ_(n=1) ^∞ (−1)^n ∫_0 ^∞ ((t/(2n+1)))^2 e^(−t) (dt/(2n+1)); where t = (2n+1)w I= Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) ∫_0 ^∞ t^2 e^(−t) dt I= Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) .2! = 2 × Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) I= 2× (π^3 /(32)) = (π^3 /(16)) ■
$$\mathrm{substitution}\:{w}\:=\:−\mathrm{ln}\:\left({x}\right)\:,\:{x}\:=\:{e}^{−{w}} \\ $$$${I}=\:\underset{\infty} {\overset{\mathrm{0}} {\int}}\:\frac{\left(−\mathrm{w}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{e}^{−\mathrm{w}} \right)^{\mathrm{2}} }\:\left(−\mathrm{e}^{−\mathrm{w}} \:\mathrm{dw}\right) \\ $$$$\mathrm{I}=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\mathrm{w}^{\mathrm{2}} .\frac{\mathrm{e}^{−\mathrm{w}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2w}} }\:\mathrm{dw}\: \\ $$$$\left[\:\frac{\mathrm{e}^{−\mathrm{w}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2w}} }\:=\:\underset{\mathrm{n}\:=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{w}} \:\right] \\ $$$$\mathrm{I}=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\left(\frac{\mathrm{t}}{\mathrm{2n}+\mathrm{1}}\right)^{\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{dt}}{\mathrm{2n}+\mathrm{1}};\: \\ $$$$\mathrm{where}\:\mathrm{t}\:=\:\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{w}\: \\ $$$$\mathrm{I}=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\: \\ $$$$\mathrm{I}=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:.\mathrm{2}!\:\:=\:\mathrm{2}\:×\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\mathrm{I}=\:\mathrm{2}×\:\:\frac{\pi^{\mathrm{3}} }{\mathrm{32}}\:=\:\frac{\pi^{\mathrm{3}} }{\mathrm{16}}\:\blacksquare\: \\ $$
Commented by  M±th+et+s last updated on 11/Jun/20
go to Q.97369
$${go}\:{to}\:{Q}.\mathrm{97369} \\ $$
Commented by bemath last updated on 13/Jun/20
greatt
$$\mathrm{greatt} \\ $$
Answered by mathmax by abdo last updated on 11/Jun/20
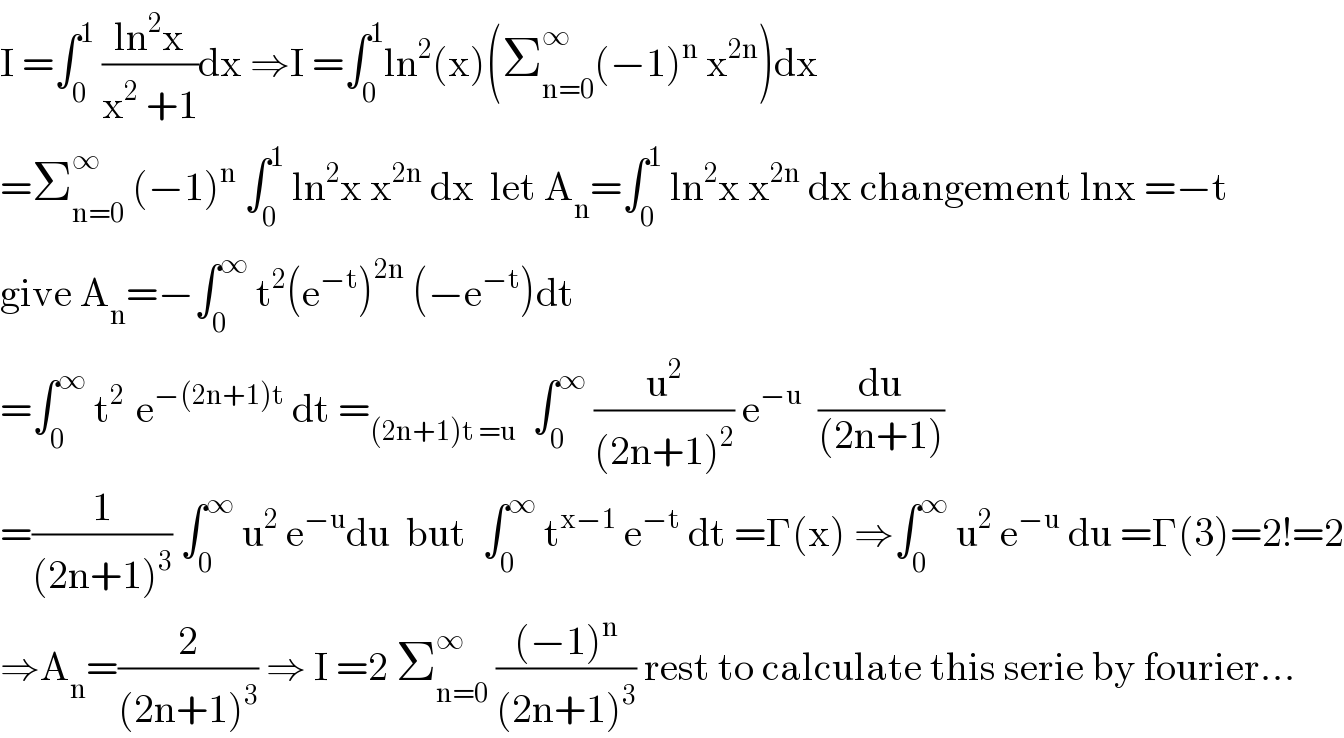
I =∫_0 ^1 ((ln^2 x)/(x^2 +1))dx ⇒I =∫_0 ^1 ln^2 (x)(Σ_(n=0) ^∞ (−1)^n x^(2n) )dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 ln^2 x x^(2n) dx let A_n =∫_0 ^1 ln^2 x x^(2n) dx changement lnx =−t give A_n =−∫_0 ^∞ t^2 (e^(−t) )^(2n) (−e^(−t) )dt =∫_0 ^∞ t^(2 ) e^(−(2n+1)t) dt =_((2n+1)t =u) ∫_0 ^∞ (u^2 /((2n+1)^2 )) e^(−u) (du/((2n+1))) =(1/((2n+1)^3 )) ∫_0 ^∞ u^2 e^(−u) du but ∫_0 ^∞ t^(x−1) e^(−t) dt =Γ(x) ⇒∫_0 ^∞ u^2 e^(−u) du =Γ(3)=2!=2 ⇒A_n =(2/((2n+1)^3 )) ⇒ I =2 Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) rest to calculate this serie by fourier...
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{x}\:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx}\:\:\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{x}\:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx}\:\mathrm{changement}\:\mathrm{lnx}\:=−\mathrm{t} \\ $$$$\mathrm{give}\:\mathrm{A}_{\mathrm{n}} =−\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \left(\mathrm{e}^{−\mathrm{t}} \right)^{\mathrm{2n}} \:\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}\:} \:\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt}\:=_{\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}\:=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{e}^{−\mathrm{u}} \:\:\frac{\mathrm{du}}{\left(\mathrm{2n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{u}} \mathrm{du}\:\:\mathrm{but}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\Gamma\left(\mathrm{x}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du}\:=\Gamma\left(\mathrm{3}\right)=\mathrm{2}!=\mathrm{2} \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\:\mathrm{I}\:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{by}\:\mathrm{fourier}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *