Question Number 184102 by paul2222 last updated on 02/Jan/23
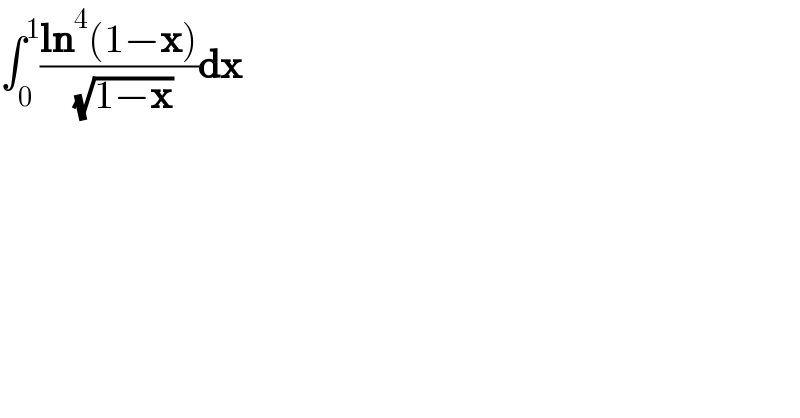
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{4}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}}\boldsymbol{\mathrm{dx}} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 03/Jan/23
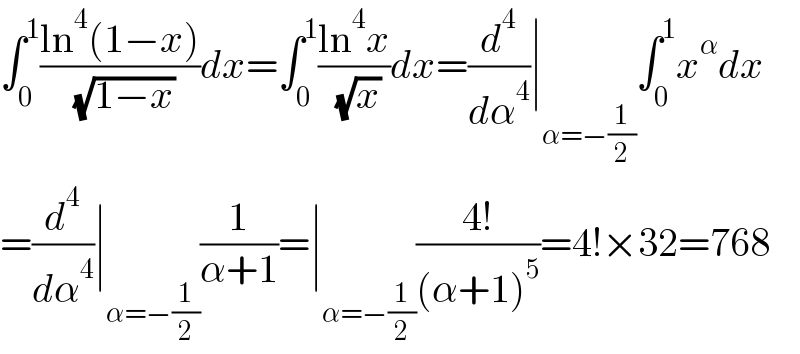
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)}{\:\sqrt{\mathrm{1}−{x}}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{4}} {x}}{\:\sqrt{{x}}}{dx}=\frac{{d}^{\mathrm{4}} }{{d}\alpha^{\mathrm{4}} }\mid_{\alpha=−\frac{\mathrm{1}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\alpha} {dx} \\ $$$$=\frac{{d}^{\mathrm{4}} }{{d}\alpha^{\mathrm{4}} }\mid_{\alpha=−\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\alpha+\mathrm{1}}=\mid_{\alpha=−\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{4}!}{\left(\alpha+\mathrm{1}\right)^{\mathrm{5}} }=\mathrm{4}!×\mathrm{32}=\mathrm{768} \\ $$
Commented by paul2222 last updated on 03/Jan/23

$$\boldsymbol{{Nice}}\:\boldsymbol{{solution}} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 03/Jan/23
����
