Menu Close

0-1-ln-lnx-x-1-ln-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 155013 by amin96 last updated on 24/Sep/21
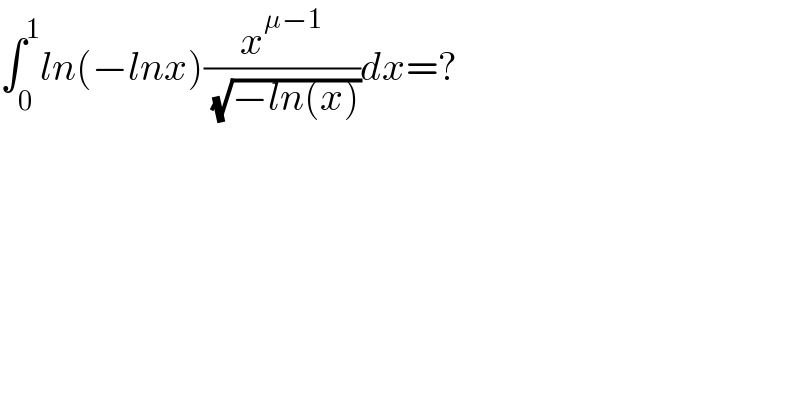
∫_0 ^1 ln(−lnx)(x^(μ−1) /( (√(−ln(x)))))dx=?
$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(−{lnx}\right)\frac{{x}^{\mu−\mathrm{1}} }{\:\sqrt{−{ln}\left({x}\right)}}{dx}=? \\ $$
Answered by mnjuly1970 last updated on 24/Sep/21
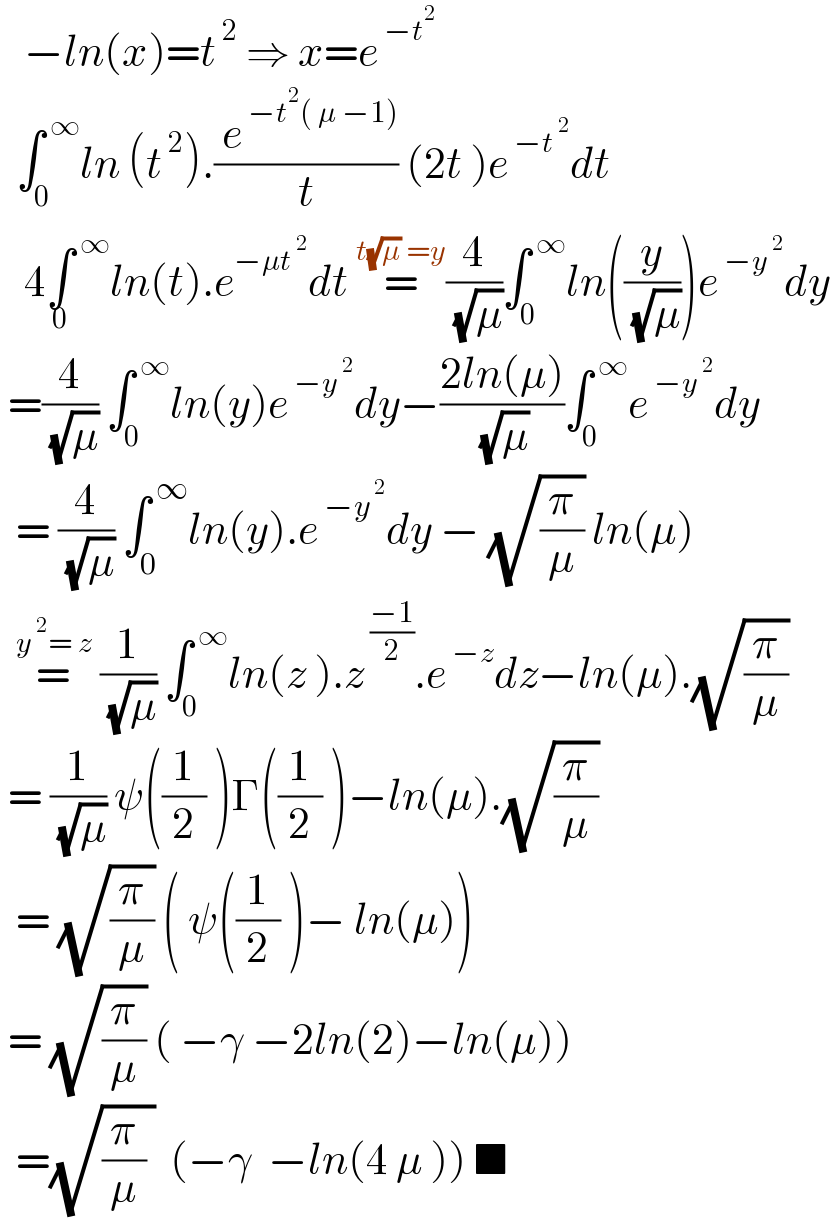
−ln(x)=t^( 2) ⇒ x=e^( −t^2 ) ∫_0 ^( ∞) ln (t^( 2) ).(( e^( −t^2 ( μ −1)) )/t) (2t )e^( −t^( 2) ) dt 4∫^( ∞) _0 ln(t).e^(−μt^( 2) ) dt =^(t(√μ) =y) (4/( (√μ)))∫_0 ^( ∞) ln((y/( (√μ))))e^( −y^( 2) ) dy =(4/( (√μ))) ∫_0 ^( ∞) ln(y)e^( −y^( 2) ) dy−((2ln(μ))/( (√μ)))∫_0 ^( ∞) e^( −y^( 2) ) dy = (4/( (√μ))) ∫_0 ^( ∞) ln(y).e^( −y^( 2) ) dy − (√(π/μ)) ln(μ) =^(y^( 2) = z) (1/( (√μ))) ∫_0 ^( ∞) ln(z ).z^( ((−1)/2)) .e^( −z) dz−ln(μ).(√(π/μ)) = (1/( (√μ))) ψ((1/2) )Γ((1/2) )−ln(μ).(√(π/μ)) = (√(π/μ)) ( ψ((1/2) )− ln(μ)) = (√(π/μ)) ( −γ −2ln(2)−ln(μ)) =(√((π/μ) )) (−γ −ln(4 μ )) ■
$$\:\:\:−{ln}\left({x}\right)={t}^{\:\mathrm{2}} \:\Rightarrow\:{x}={e}^{\:−{t}^{\mathrm{2}} } \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\infty} {ln}\:\left({t}^{\:\mathrm{2}} \right).\frac{\:{e}^{\:−{t}^{\mathrm{2}} \left(\:\mu\:−\mathrm{1}\right)} }{{t}}\:\left(\mathrm{2}{t}\:\right){e}^{\:−{t}^{\:\mathrm{2}} } {dt} \\ $$$$\:\:\:\mathrm{4}\underset{\mathrm{0}} {\int}^{\:\infty} {ln}\left({t}\right).{e}^{−\mu{t}^{\:\mathrm{2}} } {dt}\:\overset{{t}\sqrt{\mu}\:={y}} {=}\frac{\mathrm{4}}{\:\sqrt{\mu}}\int_{\mathrm{0}} ^{\:\infty} {ln}\left(\frac{{y}}{\:\sqrt{\mu}}\right){e}^{\:−{y}^{\:\mathrm{2}} } {dy} \\ $$$$\:=\frac{\mathrm{4}}{\:\sqrt{\mu}}\:\int_{\mathrm{0}} ^{\:\infty} {ln}\left({y}\right){e}^{\:−{y}^{\:\mathrm{2}} } {dy}−\frac{\mathrm{2}{ln}\left(\mu\right)}{\:\sqrt{\mu}}\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{y}^{\:\mathrm{2}} } {dy} \\ $$$$\:\:=\:\frac{\mathrm{4}}{\:\sqrt{\mu}}\:\int_{\mathrm{0}} ^{\:\infty} {ln}\left({y}\right).{e}^{\:−{y}^{\:\mathrm{2}} } {dy}\:−\:\sqrt{\frac{\pi}{\mu}}\:{ln}\left(\mu\right) \\ $$$$\:\:\overset{{y}^{\:\mathrm{2}} =\:{z}} {=}\:\frac{\mathrm{1}}{\:\sqrt{\mu}}\:\int_{\mathrm{0}} ^{\:\infty} {ln}\left({z}\:\right).{z}^{\:\frac{−\mathrm{1}}{\mathrm{2}}} .{e}^{\:−{z}} {dz}−{ln}\left(\mu\right).\sqrt{\frac{\pi}{\mu}} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\mu}}\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\:\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\:\right)−{ln}\left(\mu\right).\sqrt{\frac{\pi}{\mu}} \\ $$$$\:\:=\:\sqrt{\frac{\pi}{\mu}}\:\left(\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\:\right)−\:{ln}\left(\mu\right)\right) \\ $$$$\:=\:\sqrt{\frac{\pi}{\mu}}\:\left(\:−\gamma\:−\mathrm{2}{ln}\left(\mathrm{2}\right)−{ln}\left(\mu\right)\right) \\ $$$$\:\:=\sqrt{\frac{\pi}{\mu}\:}\:\:\left(−\gamma\:\:−{ln}\left(\mathrm{4}\:\mu\:\right)\right)\:\blacksquare \\ $$
Answered by ArielVyny last updated on 24/Sep/21
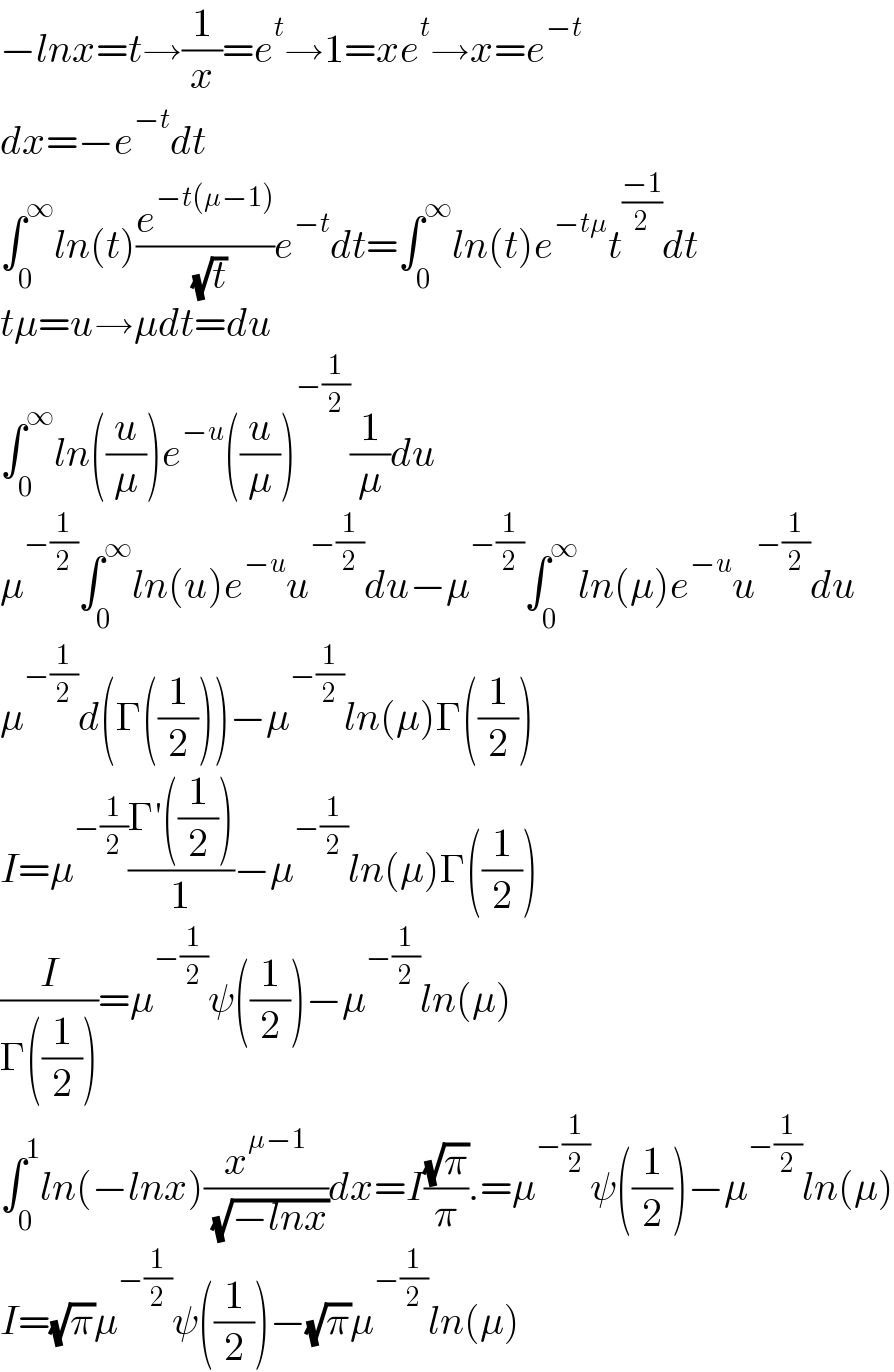
−lnx=t→(1/x)=e^t →1=xe^t →x=e^(−t) dx=−e^(−t) dt ∫_0 ^∞ ln(t)(e^(−t(μ−1)) /( (√t)))e^(−t) dt=∫_0 ^∞ ln(t)e^(−tμ) t^((−1)/2) dt tμ=u→μdt=du ∫_0 ^∞ ln((u/μ))e^(−u) ((u/μ))^(−(1/2)) (1/μ)du μ^(−(1/2)) ∫_0 ^∞ ln(u)e^(−u) u^(−(1/2)) du−μ^(−(1/2)) ∫_0 ^∞ ln(μ)e^(−u) u^(−(1/2)) du μ^(−(1/2)) d(Γ((1/2)))−μ^(−(1/2)) ln(μ)Γ((1/2)) I=μ^(−(1/2)) ((Γ′((1/2)))/1)−μ^(−(1/2)) ln(μ)Γ((1/2)) (I/(Γ((1/2))))=μ^(−(1/2)) ψ((1/2))−μ^(−(1/2)) ln(μ) ∫_0 ^1 ln(−lnx)(x^(μ−1) /( (√(−lnx))))dx=I((√π)/π).=μ^(−(1/2)) ψ((1/2))−μ^(−(1/2)) ln(μ) I=(√π)μ^(−(1/2)) ψ((1/2))−(√π)μ^(−(1/2)) ln(μ)
$$−{lnx}={t}\rightarrow\frac{\mathrm{1}}{{x}}={e}^{{t}} \rightarrow\mathrm{1}={xe}^{{t}} \rightarrow{x}={e}^{−{t}} \\ $$$${dx}=−{e}^{−{t}} {dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left({t}\right)\frac{{e}^{−{t}\left(\mu−\mathrm{1}\right)} }{\:\sqrt{{t}}}{e}^{−{t}} {dt}=\int_{\mathrm{0}} ^{\infty} {ln}\left({t}\right){e}^{−{t}\mu} {t}^{\frac{−\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$${t}\mu={u}\rightarrow\mu{dt}={du} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\frac{{u}}{\mu}\right){e}^{−{u}} \left(\frac{{u}}{\mu}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\mu}{du} \\ $$$$\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} {ln}\left({u}\right){e}^{−{u}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}−\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} {ln}\left(\mu\right){e}^{−{u}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {d}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mu\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${I}=\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \frac{\Gamma'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{1}}−\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mu\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{{I}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mu\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(−{lnx}\right)\frac{{x}^{\mu−\mathrm{1}} }{\:\sqrt{−{lnx}}}{dx}={I}\frac{\sqrt{\pi}}{\pi}.=\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mu\right) \\ $$$${I}=\sqrt{\pi}\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} \psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\sqrt{\pi}\mu^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left(\mu\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *