Question Number 150993 by talminator2856791 last updated on 17/Aug/21
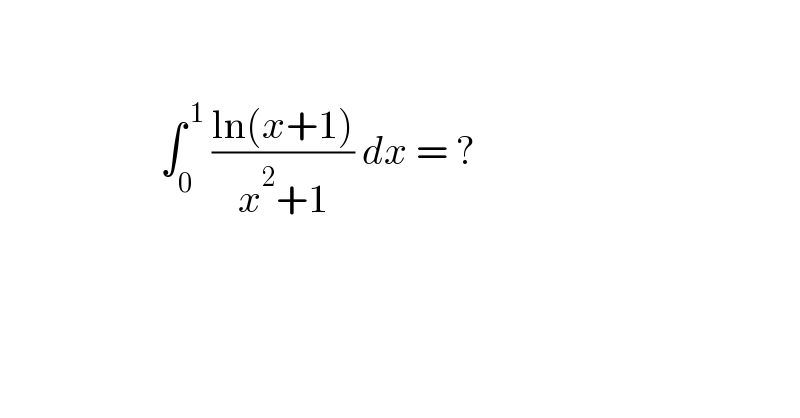
$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$
Commented by puissant last updated on 17/Aug/21

$${Q}\mathrm{150986} \\ $$
Answered by Ar Brandon last updated on 17/Aug/21
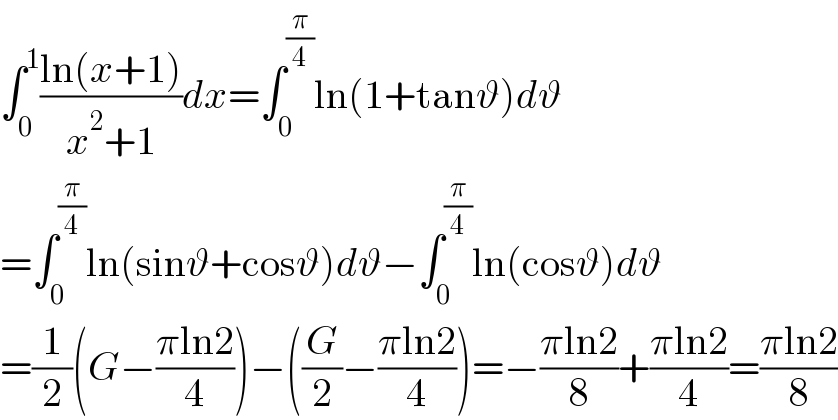
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\vartheta\right){d}\vartheta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\vartheta+\mathrm{cos}\vartheta\right){d}\vartheta−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cos}\vartheta\right){d}\vartheta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({G}−\frac{\pi\mathrm{ln2}}{\mathrm{4}}\right)−\left(\frac{{G}}{\mathrm{2}}−\frac{\pi\mathrm{ln2}}{\mathrm{4}}\right)=−\frac{\pi\mathrm{ln2}}{\mathrm{8}}+\frac{\pi\mathrm{ln2}}{\mathrm{4}}=\frac{\pi\mathrm{ln2}}{\mathrm{8}} \\ $$
