Menu Close

0-1-ln-x-2-1-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 96925 by  M±th+et+s last updated on 05/Jun/20
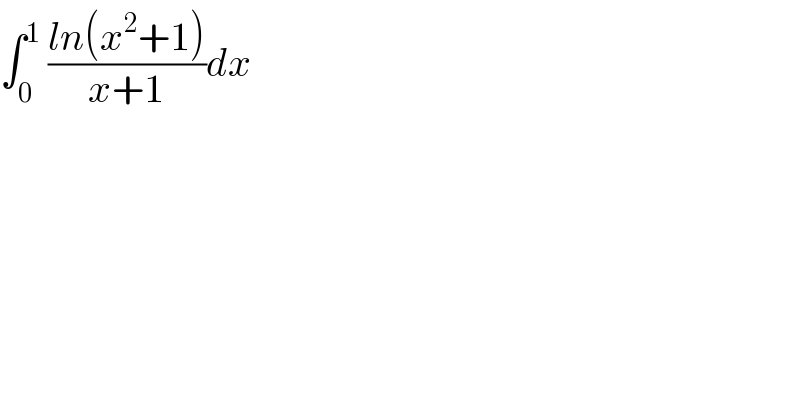
∫_0 ^1 ((ln(x^2 +1))/(x+1))dx
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$
Answered by mathmax by abdo last updated on 06/Jun/20
let f(α) =∫_0 ^1 ((ln(x^2 +α))/(x+1))dx we have f(1) =∫_0 ^1 ((ln(x^2 +1))/(x+1))dx (α>0) f^′ (α) = ∫_0 ^1 (dx/((x^2 +α)(x+1))) let decompose F(x) =(1/((x+1)(x^2 +α))) F(x) =(a/(x+1)) +((bx+c)/(x^2 +α)) we have a =(1/(1+α)) lim_(x→+∞) xF(x) =0 =a+b ⇒b =−(1/(1+α)) F(0) =(1/α) =a+(c/α) ⇒1 =αa +c ⇒c =1−αa =1−(α/(1+α)) =(1/(1+α)) ⇒ F(x) =(1/((1+α)(x+1))) +((−(1/(1+α))x +(1/(1+α)))/(x^2 +α)) =(1/(1+α)){ (1/(x+1))−(x/(x^2 +α)) +(1/(x^2 +α))} ⇒ ∫ F(x) =(1/(1+α)){ln∣x+1∣−(1/2)ln(x^2 +α) +∫ (dx/(x^2 +α))} ∫ (dx/(x^2 +α)) =_(x =(√α)u) ∫ (((√α)du)/(α(1+u^2 ))) =(1/( (√α))) arctan((x/( (√α)))) ⇒ ∫_0 ^1 F(x)dx =(1/(1+α)){ [ln∣((x+1)/( (√(x^2 +α))))∣]_0 ^1 +[(1/( (√α))) arctan((x/( (√α))))]_0 ^1 } =(1/(1+α)){ ln((2/( (√(1+α)))))−ln((1/( (√α)))) +(1/( (√α))) arctan((1/( (√α))))} ⇒ f(α) =∫ ((ln((2/( (√(1+α)) ))))/(1+α)) dα +(1/2)∫ ((lnα)/(1+α))dα +∫ ((arctan((1/( (√α)))))/((1+α)(√α))) dα +c ...be continued....
$$\mathrm{let}\:\mathrm{f}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\alpha\right)}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\:\:\left(\alpha>\mathrm{0}\right) \\ $$$$\mathrm{f}^{'} \left(\alpha\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\alpha\right)\left(\mathrm{x}+\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\alpha\right)} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} +\alpha} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{xF}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=−\frac{\mathrm{1}}{\mathrm{1}+\alpha} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\alpha}\:=\mathrm{a}+\frac{\mathrm{c}}{\alpha}\:\Rightarrow\mathrm{1}\:=\alpha\mathrm{a}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\mathrm{1}−\alpha\mathrm{a}\:=\mathrm{1}−\frac{\alpha}{\mathrm{1}+\alpha}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\alpha\right)\left(\mathrm{x}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{1}+\alpha}\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{1}+\alpha}}{\mathrm{x}^{\mathrm{2}} \:+\alpha}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha}\left\{\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\alpha}\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\alpha}\right\}\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha}\left\{\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\alpha\right)\:\:+\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\alpha}\right\} \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\alpha}\:=_{\mathrm{x}\:=\sqrt{\alpha}\mathrm{u}} \:\:\:\int\:\:\frac{\sqrt{\alpha}\mathrm{du}}{\alpha\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{\alpha}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\:\sqrt{\alpha}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha}\left\{\:\left[\mathrm{ln}\mid\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\alpha}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:+\left[\frac{\mathrm{1}}{\:\sqrt{\alpha}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\:\sqrt{\alpha}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\alpha}\left\{\:\mathrm{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\alpha}}\right)−\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\alpha}}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\alpha}}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\alpha}}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{f}\left(\alpha\right)\:=\int\:\:\frac{\mathrm{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\alpha}\:}\right)}{\mathrm{1}+\alpha}\:\mathrm{d}\alpha\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{ln}\alpha}{\mathrm{1}+\alpha}\mathrm{d}\alpha\:\:+\int\:\:\frac{\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\alpha}}\right)}{\left(\mathrm{1}+\alpha\right)\sqrt{\alpha}}\:\mathrm{d}\alpha\:\:+\mathrm{c} \\ $$$$…\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 07/Jun/20
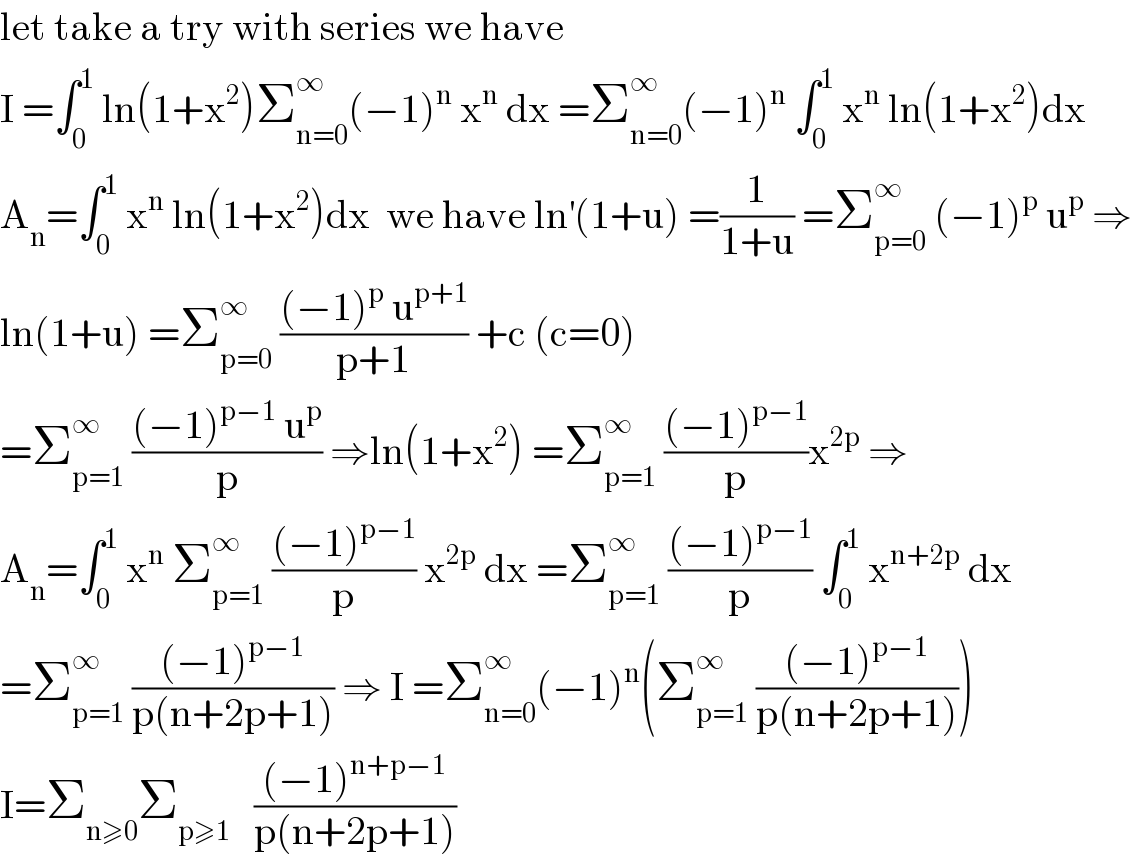
let take a try with series we have I =∫_0 ^1 ln(1+x^2 )Σ_(n=0) ^∞ (−1)^n x^n dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(1+x^2 )dx A_n =∫_0 ^1 x^n ln(1+x^2 )dx we have ln^′ (1+u) =(1/(1+u)) =Σ_(p=0) ^∞ (−1)^p u^p ⇒ ln(1+u) =Σ_(p=0) ^∞ (((−1)^p u^(p+1) )/(p+1)) +c (c=0) =Σ_(p=1) ^∞ (((−1)^(p−1) u^p )/p) ⇒ln(1+x^2 ) =Σ_(p=1) ^∞ (((−1)^(p−1) )/p)x^(2p) ⇒ A_n =∫_0 ^1 x^n Σ_(p=1) ^∞ (((−1)^(p−1) )/p) x^(2p) dx =Σ_(p=1) ^∞ (((−1)^(p−1) )/p) ∫_0 ^1 x^(n+2p) dx =Σ_(p=1) ^∞ (((−1)^(p−1) )/(p(n+2p+1))) ⇒ I =Σ_(n=0) ^∞ (−1)^n (Σ_(p=1) ^∞ (((−1)^(p−1) )/(p(n+2p+1)))) I=Σ_(n≥0) Σ_(p≥1) (((−1)^(n+p−1) )/(p(n+2p+1)))
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{with}\:\mathrm{series}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{p}} \:\mathrm{u}^{\mathrm{p}} \:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}} \:\mathrm{u}^{\mathrm{p}+\mathrm{1}} }{\mathrm{p}+\mathrm{1}}\:+\mathrm{c}\:\left(\mathrm{c}=\mathrm{0}\right)\: \\ $$$$=\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} \:\mathrm{u}^{\mathrm{p}} }{\mathrm{p}}\:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\:=\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}}\mathrm{x}^{\mathrm{2p}} \:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}}\:\mathrm{x}^{\mathrm{2p}} \:\mathrm{dx}\:=\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}+\mathrm{2p}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}\left(\mathrm{n}+\mathrm{2p}+\mathrm{1}\right)}\:\Rightarrow\:\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} }{\mathrm{p}\left(\mathrm{n}+\mathrm{2p}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{I}=\sum_{\mathrm{n}\geqslant\mathrm{0}} \sum_{\mathrm{p}\geqslant\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{p}−\mathrm{1}} }{\mathrm{p}\left(\mathrm{n}+\mathrm{2p}+\mathrm{1}\right)} \\ $$
Commented by  M±th+et+s last updated on 07/Jun/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *